题目内容
11. 如图所示是某次四驱车比赛的轨道某一段.张华控制的四驱车(可视为质点),质量m=1.0kg,额定功率为P=7W.张华的四驱车到达水平平台上A点时速度很小(可视为0),此时启动四驱车的发动机并直接使发动机的功率达到额定功率,一段时间后关闭发动机.当四驱车由平台边缘B点飞出后,恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道,且此时的速度大小为5m/s,∠COD=53°,并从轨道边缘E点竖直向上飞出,离开E以后上升的最大高度为h=0.85m.已知AB间的距离L=6m,四驱车在AB段运动时的阻力恒为1N.重力加速度g取10m/s2,不计空气阻力.sin53°=0.8,cos53°=0.6,求:
如图所示是某次四驱车比赛的轨道某一段.张华控制的四驱车(可视为质点),质量m=1.0kg,额定功率为P=7W.张华的四驱车到达水平平台上A点时速度很小(可视为0),此时启动四驱车的发动机并直接使发动机的功率达到额定功率,一段时间后关闭发动机.当四驱车由平台边缘B点飞出后,恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道,且此时的速度大小为5m/s,∠COD=53°,并从轨道边缘E点竖直向上飞出,离开E以后上升的最大高度为h=0.85m.已知AB间的距离L=6m,四驱车在AB段运动时的阻力恒为1N.重力加速度g取10m/s2,不计空气阻力.sin53°=0.8,cos53°=0.6,求:(1)四驱车运动到B点时的速度大小;
(2)发动机在水平平台上工作的时间;
(3)四驱车对圆弧轨道的最大压力.
分析 (1)小车离开B点做平抛运动,根据平行四边形定则求出水平分速度,从而得出B点的速度.
(2)对A到B的过程运用动能定理,抓住功率不变,求出发动机在水平平台上的工作时间.
(3)根据机械能守恒定律求出D点的速度,通过牛顿第二定律求出支持力的大小,从而得出压力的大小.
解答 解:(1)到达B点的速度:vB=vC•cos53°,
滑块运动到B点时的速度为:vB=5×0.6m/s=3m/s;
(2)从A到B的运动过程中有牵引力和阻力做功,
根据动能定理有:$\frac{1}{2}$mVB2=Pt-fL,代入数据解得t=1.5s;
(3)从C点运动到最高过程中,只有重力做功,机械能守恒,
由机械能守恒定律有:$\frac{1}{2}$mVC2=mg(h+R•cos53°)
圆轨道的半径R=$\frac{2}{3}$m,
设四驱车到达D点时对轨道的压力最大,
四驱车在D点速度为VD,从C到D过程中机械能守恒,
有:$\frac{1}{2}$mVD2-$\frac{1}{2}$mVC2=mgR(1-cos53°),
由牛顿第二定律得:Fmax-mg=m$\frac{{v}_{D}^{2}}{R}$,
代入数据得,四驱车对轨道的最大压力Fmax=55.5 N
答:(1)四驱车运动到B点时的速度大小为3m/s;
(2)发动机在水平平台上工作的时间为1.5s;
(3)四驱车对圆弧轨道的最大压力为55.5N.
点评 本题考查了动能定理、机械能守恒与平抛运动、圆周运动的综合,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19. 空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )
空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )
 空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )
空间某区域内存在着电场,电场线在竖直平面上的分布如图所示,一个质量为m、电量为q的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2,运动方向与水平方向之间的夹角为α,A、B两点之间的高度差与水平距离均为H.则以下判断中正确的是( )| A. | 若v2>v1,则电场力一定做正功 | |
| B. | A、B两点间的电势差U=$\frac{m({{v}_{2}}^{2}-{{v}_{1}}^{2})}{2q}$ | |
| C. | 小球由A点运动至B点,电场力做的功W=$\frac{m{{v}_{2}}^{2}}{2}$-$\frac{m{{v}_{1}}^{2}}{2}$-mgH | |
| D. | 小球运动到B点时所受重力的瞬时功率P=mgv2 |
3.一个矩形线圈在匀强磁场中匀速转动时产生的交流电的瞬时电动势表达式e=220$\sqrt{2}$sin100πt,则以下说法错误的是( )
| A. | 该交流电频率是50Hz | |
| B. | 当t=0时线圈平面恰好与中性面重合 | |
| C. | 当t=$\frac{1}{200}$s时,e有最大值 | |
| D. | 该交流电的有效值为220$\sqrt{2}$V |
1.关于电阻率的说法正确的是( )
| A. | 电阻率与导体的长度和横截面积有关 | |
| B. | 电阻率表征了材料导电能力的强弱,由导体的材料决定,且与温度有关 | |
| C. | 电阻率大的导体电阻一定大 | |
| D. | 有些合金的电阻率几乎不受温度变化的影响,用它们可做成定值电阻 |
 如图所示的电路中,已知电阻R1:R2=1:3.如果甲、乙两表均为电压表,当开关S闭合时,此时,两表的示数之比U甲:U乙=1:4;如果甲、乙两表均为电流表,当开关S断开时,两表的示数之比I甲:I乙=4:3.
如图所示的电路中,已知电阻R1:R2=1:3.如果甲、乙两表均为电压表,当开关S闭合时,此时,两表的示数之比U甲:U乙=1:4;如果甲、乙两表均为电流表,当开关S断开时,两表的示数之比I甲:I乙=4:3. 某兴趣小组在做“探究做功和物体速度变化关系”的实验前,提出以下几种猜想:①W∝v,②W∝v2,③W∝$\sqrt{v}$,….他们的实验装置如图(a)所示,PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度).在刚开始实验时,有位同学提出,不需要测出物体质量,只要测出物体从初始位置到速度传感器的距离和读出速度传感器的示数就行了,大家经过讨论采纳了该同学的建议.
某兴趣小组在做“探究做功和物体速度变化关系”的实验前,提出以下几种猜想:①W∝v,②W∝v2,③W∝$\sqrt{v}$,….他们的实验装置如图(a)所示,PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度).在刚开始实验时,有位同学提出,不需要测出物体质量,只要测出物体从初始位置到速度传感器的距离和读出速度传感器的示数就行了,大家经过讨论采纳了该同学的建议.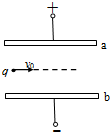 两块带有等量异种电荷的金属板靠近时,互相正对的中央区域会产生电场强度的大小、方向处处相同的电场,叫做匀强电场.如图所示,水平放置的平行金属板a、b间有一匀强电场.一电量为q=4×10-6C、质量为m=2.5×10-3kg的带电液滴,以水平初速度v0,从两板左端飞入电场,液滴恰能匀速沿水平直线方向穿出a、b间的匀强电场区域,液滴带何种电荷负(正、负),a、b金属板间匀强电场的场强为6250 N/C.
两块带有等量异种电荷的金属板靠近时,互相正对的中央区域会产生电场强度的大小、方向处处相同的电场,叫做匀强电场.如图所示,水平放置的平行金属板a、b间有一匀强电场.一电量为q=4×10-6C、质量为m=2.5×10-3kg的带电液滴,以水平初速度v0,从两板左端飞入电场,液滴恰能匀速沿水平直线方向穿出a、b间的匀强电场区域,液滴带何种电荷负(正、负),a、b金属板间匀强电场的场强为6250 N/C.