题目内容
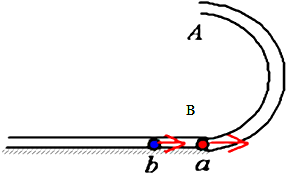 如图所示,半径为R内径很小的光滑半圆管竖直放置,和水平面相切与B处,两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时对管壁恰好没有作用力,b通过最高点A时,对管壁下部的压力为0.75mg,求:
如图所示,半径为R内径很小的光滑半圆管竖直放置,和水平面相切与B处,两个质量均为m的小球a、b以不同的速度进入管内,a通过最高点A时对管壁恰好没有作用力,b通过最高点A时,对管壁下部的压力为0.75mg,求:(1)a、b两球落地点间的距离
(2)a球在刚好进入管道B处时对管壁的压力大小.
分析:(1)根据牛顿第二定律分别求出小球在最高点A的速度大小,离开A点做平抛运动,根据平抛运动的时间和速度分别求出水平位移,从而得出a、b两球落地点间的距离.
(2)根据动能定理求出a球经过B点时的速度,运用牛顿第二定律求出轨道对球的支持力,从而得出球对管壁的压力.
(2)根据动能定理求出a球经过B点时的速度,运用牛顿第二定律求出轨道对球的支持力,从而得出球对管壁的压力.
解答:解:(1)以a球为对象,设其到达最高点时的速度为va,根据向心力公式有:
mg=m
所以:va=
.
以b球为对象,设其到达最高点时的速度为vb,根据向心力公式有:
mg-Fb=m
.
即
mg=m
所以:vb=
a、b两球脱离轨道的最高点后均做一平抛运动,所以a、b两球的水平位移分别为:
xa=
×
=2R
xb=vbt=
×
=R
故a、b两球落地点间的距离△x=xa-xb=R.
(2)对a球从B到A的过程中有
mg?2R=
mv2-
mva2
F-mg=m
F=6mg.
答:(1)a、b两球落地点间的距离为R.
(2)a球在刚好进入管道B处时对管壁的压力大小为6mg.
mg=m
| va2 |
| R |
所以:va=
| gR |
以b球为对象,设其到达最高点时的速度为vb,根据向心力公式有:
mg-Fb=m
| vb2 |
| R |
即
| 1 |
| 4 |
| vb2 |
| R |
| 1 |
| 2 |
| gR |
a、b两球脱离轨道的最高点后均做一平抛运动,所以a、b两球的水平位移分别为:
xa=
| gR |
|
xb=vbt=
| 1 |
| 2 |
| gR |
|
故a、b两球落地点间的距离△x=xa-xb=R.
(2)对a球从B到A的过程中有
mg?2R=
| 1 |
| 2 |
| 1 |
| 2 |
F-mg=m
| v2 |
| R |
F=6mg.
答:(1)a、b两球落地点间的距离为R.
(2)a球在刚好进入管道B处时对管壁的压力大小为6mg.
点评:解决本题的关键理清小球做圆周运动向心力的来源,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
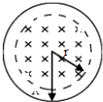 如图所示,半径为R的圆形线圈,其中心位置处半径r的虚线范围内有匀强磁场,磁场方向垂直线圈平面.若磁感应强度为B,则穿过线圈的磁通量为( )
如图所示,半径为R的圆形线圈,其中心位置处半径r的虚线范围内有匀强磁场,磁场方向垂直线圈平面.若磁感应强度为B,则穿过线圈的磁通量为( )| A、πBR2 | B、πBr2 | C、2πRB | D、2πrB? |
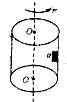 如图所示,半径为r的圆形转筒,绕其竖直中心轴OO?转动,小物块a靠在圆筒的内壁上,它与圆筒间的动摩擦因数为u,现要使小物块不下落,圆筒转动的角速度w至少为( )
如图所示,半径为r的圆形转筒,绕其竖直中心轴OO?转动,小物块a靠在圆筒的内壁上,它与圆筒间的动摩擦因数为u,现要使小物块不下落,圆筒转动的角速度w至少为( )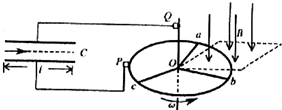 如图所示,半径为r的金属圆环置于水平面内,三条电阻均为R的导体杆Oa、Ob和Oc互成120°连接在圆心O和圆环上,圆环绕经过圆心O的竖直金属转轴以大小为ω的角速度按图中箭头方向匀速转动.一方向竖直向下的匀强磁场区与圆环所在平面相交,相交区域为一如图虚线所示的正方形(其一个顶点位于O处).C为平行板电容器,通过固定的电刷P和Q接在圆环和金属转轴上,电容器极板长为l,两极板的间距为d.有一细电子束沿两极板间的中线以大小为v0(
如图所示,半径为r的金属圆环置于水平面内,三条电阻均为R的导体杆Oa、Ob和Oc互成120°连接在圆心O和圆环上,圆环绕经过圆心O的竖直金属转轴以大小为ω的角速度按图中箭头方向匀速转动.一方向竖直向下的匀强磁场区与圆环所在平面相交,相交区域为一如图虚线所示的正方形(其一个顶点位于O处).C为平行板电容器,通过固定的电刷P和Q接在圆环和金属转轴上,电容器极板长为l,两极板的间距为d.有一细电子束沿两极板间的中线以大小为v0(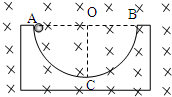 如图所示,半径为R的半圆形槽放在粗糙的水平地面上,槽内部光滑,其质量为M.匀强磁场与槽面垂直向内,将质量为m的带电小球自槽口A处由静止释放,小球到达槽最低点C时,恰好对槽无压力.整个过程中M对地始终静止,问:
如图所示,半径为R的半圆形槽放在粗糙的水平地面上,槽内部光滑,其质量为M.匀强磁场与槽面垂直向内,将质量为m的带电小球自槽口A处由静止释放,小球到达槽最低点C时,恰好对槽无压力.整个过程中M对地始终静止,问: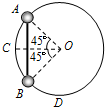 (2013?淮安模拟)如图所示,半径为R的光滑圆环固定在竖直平面内,O是圆心,虚线OC水平,D是圆环最低点.两个质量均为m的小球A、B套在圆环上,两球之间用轻杆相连,从图示位置由静止释放,则( )
(2013?淮安模拟)如图所示,半径为R的光滑圆环固定在竖直平面内,O是圆心,虚线OC水平,D是圆环最低点.两个质量均为m的小球A、B套在圆环上,两球之间用轻杆相连,从图示位置由静止释放,则( )