题目内容
 一质量为m的物体放在水平面上,在与水平面成θ角的力F的作用下由静止开始运动,物体与水平面间的动摩擦因数为μ,如图所示,则物体所受摩擦力 Ff和弹力FN( )
一质量为m的物体放在水平面上,在与水平面成θ角的力F的作用下由静止开始运动,物体与水平面间的动摩擦因数为μ,如图所示,则物体所受摩擦力 Ff和弹力FN( )分析:对物体进行受力分析,把拉力正交分解,用μ表示摩擦力,
根据竖直方向平衡列出等式求解.
根据竖直方向平衡列出等式求解.
解答:解:对物体进行受力分析:

把拉力在水平方向和竖直方向分解,
根据竖直方向平衡得出:
mg=Fsinθ+FN
FN=mg-Fsinθ
所以FN<mg
根据滑动摩擦力公式得出:
Ff=μFN=μ(mg-Fsinθ)
所以Ff<μmg.
故选A.

把拉力在水平方向和竖直方向分解,
根据竖直方向平衡得出:
mg=Fsinθ+FN
FN=mg-Fsinθ
所以FN<mg
根据滑动摩擦力公式得出:
Ff=μFN=μ(mg-Fsinθ)
所以Ff<μmg.
故选A.
点评:处理该问题的思路是对物体进行受力分析,运用正交分解和牛顿第二定律解决问题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
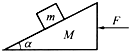 如图所示,在光滑水平面上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )
如图所示,在光滑水平面上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用一水平力F推斜劈,恰使物体m与斜劈间无相对滑动,则斜劈对物块m的弹力大小为( )| A、mgcosα | ||
B、
| ||
C、
| ||
D、
|
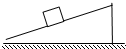 一质量为m的物体放在粗糙斜面上,处于静止状态,物体与斜面间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
一质量为m的物体放在粗糙斜面上,处于静止状态,物体与斜面间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )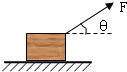 一质量为m的物体放在水平地面上,在与水平面成θ角的力F的作用下由静止开始沿水平地面向右运动,物体与水平地面之间的动摩擦因数为μ,如图所示.则物体所受的摩擦力f( )
一质量为m的物体放在水平地面上,在与水平面成θ角的力F的作用下由静止开始沿水平地面向右运动,物体与水平地面之间的动摩擦因数为μ,如图所示.则物体所受的摩擦力f( ) 如图一倾角θ=37°的斜面在B点以上是光滑的,B点以下是粗糙的(且动摩擦因数μ=0.8),一质量为m的物体放在斜面上A处并用水平力拉住使之静止不动(g取10m/s2).
如图一倾角θ=37°的斜面在B点以上是光滑的,B点以下是粗糙的(且动摩擦因数μ=0.8),一质量为m的物体放在斜面上A处并用水平力拉住使之静止不动(g取10m/s2).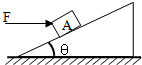 一质量为m的物体放在固定的粗糙斜面上保持静止,现用水平力F推m,如图所示,当F由零逐渐增加但物体m仍保持静止状态的情况下,则( )
一质量为m的物体放在固定的粗糙斜面上保持静止,现用水平力F推m,如图所示,当F由零逐渐增加但物体m仍保持静止状态的情况下,则( )