��Ŀ����
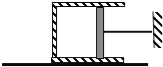
����Ŀ����ͼ��ʾ����xoyƽ���ڣ���һ��Բ�������ֱ��AB��x���غϣ�Բ��O��������Ϊ��2a��0������뾶Ϊa�����������ų�����y���ֱ��x=3a֮������������ڴ��ڴ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB��һ����Ϊm�������Ϊq�Ĵ���������Ӵ�y����ij������ų�����������������
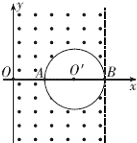
��1�������ӵij��ٶȷ�����y������н�Ϊ60�㣬�����Ӳ�����Բ��������ܵ���B�㣬�����ӵij��ٶȴ�Сv1��
��2�������ӵij��ٶȷ�����y������н�Ϊ60�㣬�ڴų����˶���ʱ��Ϊ![]() ��������Ҳ�ܵ���B�㣬�����ӵij��ٶȴ�Сv2��
��������Ҳ�ܵ���B�㣬�����ӵij��ٶȴ�Сv2��
��3�������ӵij��ٶȷ�����y�ᴹֱ�������Ӵ�O�����һ�ξ���x�ᣬ�����ӵ���С���ٶ�vm��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
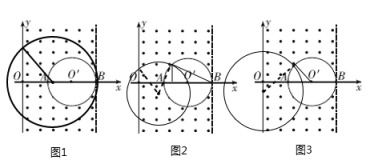
�����������1�����Ӳ�����Բ��������ܵ���B�㣬�����ӵ���B��ʱ�ٶ���ֱ���£�Բ�ı���x���������ϣ���������Բ���˶��İ뾶Ϊr1����ͼ1���ɼ��ι�ϵ�ã�r1sin30��=3a��r1 ��2����
���������������ṩ����������Բ���˶�����������![]() ������ӵİ뾶Ϊ��
������ӵİ뾶Ϊ��![]() ��2����
��2����
��ã�![]() ��1����
��1����
��2�������ڴų��е��˶�����Ϊ��![]() ���������ڴų��е��˶��켣��ͼ2��ʾ��Բ�Ľ�ΪΪ��
���������ڴų��е��˶��켣��ͼ2��ʾ��Բ�Ľ�ΪΪ��![]() ��1����
��1����
���ӵ���B����ٶ���x��н� ��=30�� ��1����
��������Բ���˶��İ뾶Ϊr2���ɼ��ι�ϵ�ã� 3a=2r2sin30��+2acos30��cos30�� ��1����
���������������ṩ����������Բ���˶�����������![]() ������ӵİ뾶Ϊ��
������ӵİ뾶Ϊ��![]()
��ã�![]() ��1����
��1����
��3�������Ӵ�C������Բ������O��C��O��A�н�Ϊ�����켣Բ��Ӧ�İ뾶Ϊr����ͼ3��ʾ���ɼ��ι�ϵ�ã�2a=rsin��+acos�� ��1����
�ʵ���=60��ʱ���뾶��СΪ![]() ��1����
��1����
���������������ṩ����������Բ���˶�����������![]() ��
��
������ӵİ뾶Ϊ��![]() ��1����
��1����
��ã�![]() ��1����
��1����