题目内容
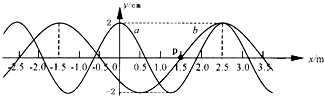
有两列简谐横波a、b在同一媒质中沿x轴正方向传播，波速均为v=2.5m/s．在t=0时，两列波的波峰正好在x=2.5m处重合（如图）．那么两列波的周期Ta和Tb之比为
5：8
5：8
；t=0时两列波的波峰重合处的所有位置X=x=（2.5±20k）（k=0，1，2，3，…）
x=（2.5±20k）（k=0，1，2，3，…）
m．分析：由图读出两列波的波长，由波速公式求解周期之比．运用数学知识，求出位置坐标的通项．
解答：解；（1）从图中可以看出两列波的波长分别为λa=2.5m，λb=4.0m，波长之比λa：λb=5：8．由波速公式v=
，波速相同，则有周期Ta和Tb之比：Ta：Tb=λa：λb=5：8．
（2）两列波波长的最小整数公倍数为S=20m，则t=0时，两列波的波峰重合处的所有位置为
x=（2.5±20k）m，k=0，1，2，3，…
故答案为：5：8，x=（2.5±20k） （k=0，1，2，3，…）
| λ |
| T |
（2）两列波波长的最小整数公倍数为S=20m，则t=0时，两列波的波峰重合处的所有位置为
x=（2.5±20k）m，k=0，1，2，3，…
故答案为：5：8，x=（2.5±20k） （k=0，1，2，3，…）
点评：本题考查运用数学知识解决物理问题的能力．对于多解问题，往往要分析规律，列出通项表达式，解题时要防止漏解．
练习册系列答案
走进文言文系列答案
相关题目
