题目内容
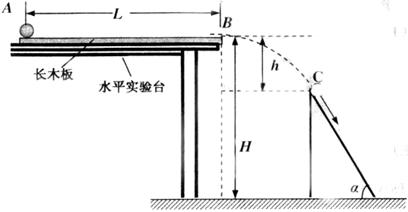
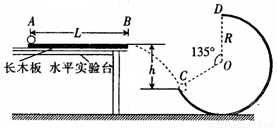
 如图所示,长木板固定在水平实验台上,在水平实验台右端地面上竖直放有一粗糙的被截去八分之三(即圆心角为135°)的圆轨道,轨道半径为R;放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动,运动到长木板边缘B处撤去水平恒力F,小球水平抛出后恰好落在圆轨道C处,速度方向沿C处的切线方向,且刚好能到达圆轨道的最高点D处.已知小球的质量为m,小球与水平长木板间的动摩擦因数为μ,长木板AB长为L,B、C两点间的竖直高度为h,求:
如图所示,长木板固定在水平实验台上,在水平实验台右端地面上竖直放有一粗糙的被截去八分之三(即圆心角为135°)的圆轨道,轨道半径为R;放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动,运动到长木板边缘B处撤去水平恒力F,小球水平抛出后恰好落在圆轨道C处,速度方向沿C处的切线方向,且刚好能到达圆轨道的最高点D处.已知小球的质量为m,小球与水平长木板间的动摩擦因数为μ,长木板AB长为L,B、C两点间的竖直高度为h,求:(1)B、C两点间的水平距离x
(2)水平恒力F的大小
(3)小球在圆轨道上运动时克服摩擦力做的功.
分析:(1)小球从抛出到C过程做平抛运动,已知C的速度方向和竖直分位移,根据平抛运动的分位移和分速度公式列式求解即可;
(2)对小球从A到B的过程运用动能定理列式求解即可;
(3)小球恰好经过圆轨道最高点,重力提供向心力,根据牛顿第二定律列式求解最高点速度;然后对从C到最高点过程运用动能定理列式求解克服摩擦力做的功.
(2)对小球从A到B的过程运用动能定理列式求解即可;
(3)小球恰好经过圆轨道最高点,重力提供向心力,根据牛顿第二定律列式求解最高点速度;然后对从C到最高点过程运用动能定理列式求解克服摩擦力做的功.
解答:解:(1)小球落在C处时,有:vy=
由几何知识有vx=vy=
小球从B运动到C的时间t=
所以有:x=vxt=
?
=2h.
(2)小球从A到B,由动能定理得:
F
-μmgL=
m
解得:F=μmg+
.
(3)由于小球刚好能到达圆轨道的最高点D,则在D处有:mg=m
小球从C沿圆轨道到D,由功能关系得:
mvC2=
mvD2+mg×
R+W
又vC=
vX=2
∴W=2mgh-
mgR.
答:(1)B、C两点间的水平距离x为2h;
(2)水平恒力F的大小为μmg+
;
(3)小球在圆轨道上运动时克服摩擦力做的功为2mgh-
mgR.
| 2gh |
由几何知识有vx=vy=
| 2gh |
小球从B运动到C的时间t=
|
所以有:x=vxt=
| 2gh |
|
(2)小球从A到B,由动能定理得:
F
| L |
| 1 |
| 2 |
| v | 2 x |
解得:F=μmg+
| mgh |
| L |
(3)由于小球刚好能到达圆轨道的最高点D,则在D处有:mg=m
| vD2 |
| R |
小球从C沿圆轨道到D,由功能关系得:
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
又vC=
| 2 |
| gh |
∴W=2mgh-
3+
| ||
| 2 |
答:(1)B、C两点间的水平距离x为2h;
(2)水平恒力F的大小为μmg+
| mgh |
| L |
(3)小球在圆轨道上运动时克服摩擦力做的功为2mgh-
3+
| ||
| 2 |
点评:本题关键明确物体的运动规律,然后分阶段结合动能定理、平抛运动、牛顿第二定律的相关公式列式求解.

练习册系列答案
相关题目
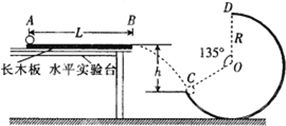 如图所示,长木板固定在水平实验台上,在水平实验台右端地面上竖直放有一光滑的被截去八分之三(即圆心角为135°)的圆轨道;放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动,运动到长木板边缘B处撤去水平恒力F,小球水平抛出后恰好落在圆轨道C处,速度方向沿C处的切线方向,且刚好能到达圆轨道的最高点D处.已知小球的质量为m,小球与水平长木板间的动摩擦因数为μ,长木板AB长为L,B、C两点间的竖直高度为h,求:
如图所示,长木板固定在水平实验台上,在水平实验台右端地面上竖直放有一光滑的被截去八分之三(即圆心角为135°)的圆轨道;放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动,运动到长木板边缘B处撤去水平恒力F,小球水平抛出后恰好落在圆轨道C处,速度方向沿C处的切线方向,且刚好能到达圆轨道的最高点D处.已知小球的质量为m,小球与水平长木板间的动摩擦因数为μ,长木板AB长为L,B、C两点间的竖直高度为h,求: