题目内容
 两平行金属板A、B水平放置,一个质量为m=5×10-6kg 的带电微粒以v0=2m/s的水平速度从两板正中位置射入电场,如图所示,A、B间距为d=4cm,板长l=10crn.(g取10m/s2 )
两平行金属板A、B水平放置,一个质量为m=5×10-6kg 的带电微粒以v0=2m/s的水平速度从两板正中位置射入电场,如图所示,A、B间距为d=4cm,板长l=10crn.(g取10m/s2 )(1)当A、B间电压UAB=1.0×103V时,微粒恰好不发生偏转,求该微粒的电性和电荷量.
(2)令B板接地,要使该微粒能穿过电场,求A板的电势.
分析:(1)当A、B间电压UAB=1.0×103V时,微粒恰好不发生偏转,则知微粒做匀速直线运动,重力与电场力平衡,即可分析微粒的电性,由平衡条件求出电量.
(2)研究临界情况:微粒刚好从B板右端和A板右端射出时的情况.微粒在水平方向做匀速直线运动,竖直方向做初速度为0的匀加速运动,由运动学公式求出加速度,由牛顿第二定律求出A板的电势.
(2)研究临界情况:微粒刚好从B板右端和A板右端射出时的情况.微粒在水平方向做匀速直线运动,竖直方向做初速度为0的匀加速运动,由运动学公式求出加速度,由牛顿第二定律求出A板的电势.
解答:解:(1)板间场强为 E=
=
=2.5×104V/m
根据题意,当A、B间电压UAB=1.0×103V时,微粒恰好不发生偏转,则知微粒做匀速直线运动,重力与电场力平衡,可知该微粒带负电,有
qE=mg
得 q=
=
=2.0×10-9C
(2)若微粒刚好从B板右端射出时
运动时间 t=
竖直位移
=
a1t2
解得加速度 a1=16m/s2
设A板电势为φ1时,由加速度a1=
得到 a1=g-
解得φ1=-600V
微粒刚好从A板右端射出时,设A板电势为φ2,同理有
运动时间 t=
竖直位移
=
a2t2
解得 a2=16m/s2
而a2=
-g,解得 φ2=2600V
则要使微粒从两板间飞出,A板的电势φ的取值为:-600V≤φ≤2600V
答:(1)该微粒的电性是负电荷,电荷量为2×10-9C.
(2)令B板接地,要使该微粒能穿过电场,A板的电势为-600V≤φ≤2600V.
| U |
| d |
| 1.0×103 |
| 4×10-2 |
根据题意,当A、B间电压UAB=1.0×103V时,微粒恰好不发生偏转,则知微粒做匀速直线运动,重力与电场力平衡,可知该微粒带负电,有
qE=mg
得 q=
| mg |
| E |
| 5×10-6×10 |
| 2.5×104 |
(2)若微粒刚好从B板右端射出时
运动时间 t=
| L |
| v0 |
竖直位移
| d |
| 2 |
| 1 |
| 2 |
解得加速度 a1=16m/s2
设A板电势为φ1时,由加速度a1=
mg-q
| ||
| m |
| qφ1 |
| md |
解得φ1=-600V
微粒刚好从A板右端射出时,设A板电势为φ2,同理有
运动时间 t=
| L |
| v0 |
竖直位移
| d |
| 2 |
| 1 |
| 2 |
解得 a2=16m/s2
而a2=
| qφ2 |
| md |
则要使微粒从两板间飞出,A板的电势φ的取值为:-600V≤φ≤2600V
答:(1)该微粒的电性是负电荷,电荷量为2×10-9C.
(2)令B板接地,要使该微粒能穿过电场,A板的电势为-600V≤φ≤2600V.
点评:本题第1问是匀速直线运动,属于力平衡问题;第2问是类平抛运动,难点是分析隐含的临界情况,运用运动的分解法求解电势的范围.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v0=10
如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v0=10
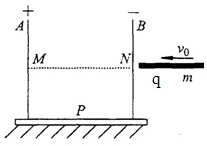

 如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v=10
如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v=10 m/s的速度由右边小孔水平滑入“U”形框架中,设绝缘棒的电荷量对“U”形框架内的电场没有影响.问:
m/s的速度由右边小孔水平滑入“U”形框架中,设绝缘棒的电荷量对“U”形框架内的电场没有影响.问: