题目内容
 如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v0=10
如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v0=10| 3 |
(1)橡胶棒刚好全部进入“U”形框架内的加速度
(2)橡胶棒刚好全部进入“U”形框架内的速度.
(3)橡胶棒与“U”形框架相互作用过程中增加的最大电势能.
分析:(1)由公式E=
求出金属板间的电场强度,根据牛顿第二定律求解橡胶棒刚好全部进入“U”形框架内的加速度.
(2)由动能定理求解橡胶棒刚好全部进入“U”形框架内的速度.
(3)根据能量守恒求解橡胶棒与“U”形框架相互作用过程中增加的最大电势能.
| U |
| d |
(2)由动能定理求解橡胶棒刚好全部进入“U”形框架内的速度.
(3)根据能量守恒求解橡胶棒与“U”形框架相互作用过程中增加的最大电势能.
解答:解:(1)金属板间的电场强度为E=
=
V/m=1.5×106V/m
由牛顿第二定律得:a=
=
m/s2=7.5×103m/s2
(2)设带电橡胶棒刚好全部进入“U”形框架时,则由动能定理:
-
L=
mv2-
m
解得:v=
=
m/s=0m/s
(3)增加电势能的最大值等于动能减小的最大值:
△Ep=△Ek=
m
=
×0.01×300J=1.5J
答:
(1)橡胶棒刚好全部进入“U”形框架内的加速度为7.5×103m/s2.
(2)橡胶棒刚好全部进入“U”形框架内的速度是0.
(3)橡胶棒与“U”形框架相互作用过程中增加的最大电势能是1.5J.
| U |
| d |
| 150×103 |
| 0.1 |
由牛顿第二定律得:a=
| qE |
| m |
| 5×10-5×1.5×106 |
| 0.01 |
(2)设带电橡胶棒刚好全部进入“U”形框架时,则由动能定理:
-
| qE |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得:v=
|
(10
|
(3)增加电势能的最大值等于动能减小的最大值:
△Ep=△Ek=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
答:
(1)橡胶棒刚好全部进入“U”形框架内的加速度为7.5×103m/s2.
(2)橡胶棒刚好全部进入“U”形框架内的速度是0.
(3)橡胶棒与“U”形框架相互作用过程中增加的最大电势能是1.5J.
点评:本题文字较多,题干较长,要善于抓住有效信息,实质是匀减速运动的问题.

练习册系列答案
相关题目
 (2004?江苏)如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为0.5m,横跨在导线框上的导体棒ab的电阻r=1.0Ω,接在NQ间的电阻R=4.OΩ,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.
(2004?江苏)如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为0.5m,横跨在导线框上的导体棒ab的电阻r=1.0Ω,接在NQ间的电阻R=4.OΩ,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.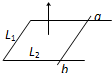 如图所示,U形导线框固定在水平面上,右端放有质量为m的金属棒ab,ab与导轨间的动摩擦因数为μ,它们围成的矩形边长分别为L1、L2,回路的总电阻为R.从t=0时刻起,在竖直向上方向加一个随时间均匀变化的匀强磁场B=kt,(k>0)那么在t=
如图所示,U形导线框固定在水平面上,右端放有质量为m的金属棒ab,ab与导轨间的动摩擦因数为μ,它们围成的矩形边长分别为L1、L2,回路的总电阻为R.从t=0时刻起,在竖直向上方向加一个随时间均匀变化的匀强磁场B=kt,(k>0)那么在t=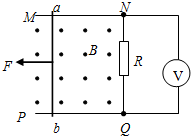 如图所示,U形导线框MNQP水平放置在 磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.求:
如图所示,U形导线框MNQP水平放置在 磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.求: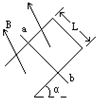 如图所示,U形导体框架宽L=1m,与水平面成α=30°角倾斜放置在匀强磁场中,磁感应强度B=0.2T,垂直框面向上.在框架上垂直框边放有一根质量m=0.2kg、有效电阻R=0.1Ω的导体棒ab,从静止起沿框架无摩擦下滑,设框架电阻不计,框边有足够长,取g=10m/s2,求:ab棒下滑的最大速度vm.
如图所示,U形导体框架宽L=1m,与水平面成α=30°角倾斜放置在匀强磁场中,磁感应强度B=0.2T,垂直框面向上.在框架上垂直框边放有一根质量m=0.2kg、有效电阻R=0.1Ω的导体棒ab,从静止起沿框架无摩擦下滑,设框架电阻不计,框边有足够长,取g=10m/s2,求:ab棒下滑的最大速度vm.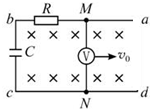 如图所示,U形线框abcd处于匀强磁场中,磁场的磁感应强度为B,方向垂直于纸面向里,长度为L的直导线MN中间串有一个电压表跨接在ab与cd上且与ab垂直,它们之间的接触是完全光滑的,R为电阻,C为电容器.现令MN以速度v0向右匀速运动,用U表示电压表的读数,Q表示电容器所带电荷量,C表示电容器的电容,F表示对MN的拉力,设电压表的体积很小,其中线圈切割磁感线对MN间的电压的影响可以忽略不计,则( )
如图所示,U形线框abcd处于匀强磁场中,磁场的磁感应强度为B,方向垂直于纸面向里,长度为L的直导线MN中间串有一个电压表跨接在ab与cd上且与ab垂直,它们之间的接触是完全光滑的,R为电阻,C为电容器.现令MN以速度v0向右匀速运动,用U表示电压表的读数,Q表示电容器所带电荷量,C表示电容器的电容,F表示对MN的拉力,设电压表的体积很小,其中线圈切割磁感线对MN间的电压的影响可以忽略不计,则( )