题目内容
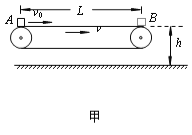
【题目】如图甲所示为车站使用的水平传送装置的示意图。绷紧的传送带长度L=6.0m，以v=6.0m/s的恒定速率运行，传送带的水平部分AB距离水平地面的高度h=0.45m。现有一行李箱（可视为质点）质量m=10kg，以v0＝5.0m/s的水平初速度从A端滑上传送带，被传送到B端时没有被及时取下，行李箱从B端水平抛出，行李箱与传送带间的动摩擦因数μ＝0.20，不计空气阻力，重力加速度g取10 m/s2。试分析求解：
（1）行李箱从传送带上A端运动到B端过程中摩擦力对行李箱冲量的大小；
（2）为运送该行李箱电动机多消耗的电能；
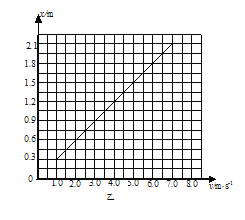
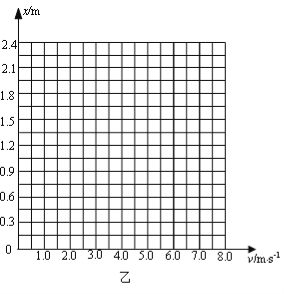
（3）若传送带的速度v可在0～8.0m/s之间调节，仍以v0的水平初速度从A端滑上传送带，且行李箱滑到B端均能水平抛出。请你在图乙中作出行李箱从B端水平抛出到落地点的水平距离x与传送带速度v的关系图象。（要求写出作图数据的分析过程）
【答案】（1）10Ns（2）60J（3）图象见答案
【解析】
试题分析：（1）行李箱刚滑上传送带时做匀加速直线运动，设行李箱受到的摩擦力为Ff
根据牛顿第二定律有 Ff＝μmg＝ma
解得 a＝μg＝2.0 m/s2
设行李箱速度达到v＝6.0 m/s时的位移为s1
v2－v02＝2as1
s1＝
＝2.75m
即行李箱在传动带上能加速达到传送带的速度6.0 m/s
设摩擦力的冲量为If，依据动量定理If＝mv－mv0
解得If＝10Ns
说明：用其他方法求解，正确的也给分。没有判断速度能达到6.0 m/s的过程扣1分。
（2）在行李箱匀加速运动的过程中，传送带上任意一点移动的长度s＝vt＝3 m
行李箱与传送带摩擦产生的内能Q＝μmg（s-s1） （1分）
行李箱增加的动能ΔEk＝
m（v2－v02） （1分）
设电动机多消耗的电能为E，根据能量转化与守恒定律得
E＝ΔEk+Q
解得 E＝60J （1分）
（3）若行李箱一直做匀减速直线运动，到达右端的速度：
v1＝
＝1.0m/s
若行李箱一直做匀加速直线运动，到达右端的速度：
v2＝
＝7.0m/s
若传送带的速度v < v1，行李箱将一直做匀减速运动，到达右端后滑出，之后做平抛运动，时间
，水平位移x＝v1t = 0.3m
若传送带的速度v1< v < v0，行李箱将先做匀减速运动，达到与传速带共速后匀速滑出，行李箱的水平位移
，式中为恒量，即水平位移x与传送带速度v成正比。
若传送带的速度v0< v < v2，行李箱将先做匀加速运动，达到与传速带共速后匀速滑出，行李箱的水平位移，式中为恒量，即水平位移x与传送带速度v成正比。
若传送带的速度v>7.0m/s时，行李箱一直做匀加速运动，到达右端后滑出，水平位移x＝v2t＝2.1 m
行李箱从传送带水平抛出后的x-v图象如答图所示。
