题目内容
 如图所示,P为位于某一高度处的质量为m的小物块(可视为质点),B为位于水平地面上的质量为M的特殊长平板,
如图所示,P为位于某一高度处的质量为m的小物块(可视为质点),B为位于水平地面上的质量为M的特殊长平板,| m |
| M |
| 1 |
| 10 |
(1)物块P从开始自由下落到再次回到初始位置所经历的时间.
(2)在这段时间内B所通过的位移的大小.
分析:(1)物块P在进入“相互作用区域”之前做自由落体运动,加速度为g,进入“相互作用区域”之后做匀减速直线运动,根据牛顿第二定律求出加速度.根据两个过程速度的关系求解P从进入“相互作用区域”到离木板最近过程所经历的时间,根据对称性求出物块P从开始自由下落到再次回到初始位置所经历的时间.
(2)对于B的运动过程分三段;
①在P从开始下落到进入“相互作用区域”的时间t0内,B物体做匀减速直线运动,由速度公式求出末速度.
②在P进入到离开“相互作用区域”的过程,B物体做匀减速直线运动,求出末速度.
③在P从离开“相互作用区域”到回到初位置的t0时间内,B做匀减速直线运动,再求出末速度.
根据三个过程的初速度、末速度和时间,由平均速度和时间求出总位移.
(2)对于B的运动过程分三段;
①在P从开始下落到进入“相互作用区域”的时间t0内,B物体做匀减速直线运动,由速度公式求出末速度.
②在P进入到离开“相互作用区域”的过程,B物体做匀减速直线运动,求出末速度.
③在P从离开“相互作用区域”到回到初位置的t0时间内,B做匀减速直线运动,再求出末速度.
根据三个过程的初速度、末速度和时间,由平均速度和时间求出总位移.
解答:解:
(1)对于P,取向下方向为正方向,对于B取水平向右为正方向.
物块P在进入“相互作用区域”之前,P、B的加速度分别是aP=g,aB=-μg
物块P在进入“相互作用区域”之后,P、B的加速度分别是aP′=
=-50g,aB′=-
=-6.1g
设P从进入“相互作用区域”到离木板最近过程所经历的时间为t,则
aPt0+aP′t=0
解得t=0.04s
根据对称性得到物块P从开始自由下落到再次回到初始位置所经历的时间T=2(t0+t)=4.08s
(2)在P从开始下落到进入“相互作用区域”的时间t0内,B物体做匀减速直线运动,末速度为v1=v0+aBt0=10-0.2×2(m/s)=9.6m/s
在P进入到离开“相互作用区域”的2t时间内,B仍做匀减速直线运动,速度减到v2=v1+2aBt=9.5m/s
在P从离开“相互作用区域”到回到初位置的t0时间内,B做匀减速直线运动,末速度为v3=v2+aBt0=9.1m/s
所以在这段时间内B所通过的位移的大小为
x=
t0+
?2t+
t0=36m.
答:(1)物块P从开始自由下落到再次回到初始位置所经历的时间是4.08s;
(2)在这段时间内B所通过的位移的大小为36m.
(1)对于P,取向下方向为正方向,对于B取水平向右为正方向.
物块P在进入“相互作用区域”之前,P、B的加速度分别是aP=g,aB=-μg
物块P在进入“相互作用区域”之后,P、B的加速度分别是aP′=
| mg-F |
| m |
| μ(Mg+F) |
| M |
设P从进入“相互作用区域”到离木板最近过程所经历的时间为t,则
aPt0+aP′t=0
解得t=0.04s
根据对称性得到物块P从开始自由下落到再次回到初始位置所经历的时间T=2(t0+t)=4.08s
(2)在P从开始下落到进入“相互作用区域”的时间t0内,B物体做匀减速直线运动,末速度为v1=v0+aBt0=10-0.2×2(m/s)=9.6m/s
在P进入到离开“相互作用区域”的2t时间内,B仍做匀减速直线运动,速度减到v2=v1+2aBt=9.5m/s
在P从离开“相互作用区域”到回到初位置的t0时间内,B做匀减速直线运动,末速度为v3=v2+aBt0=9.1m/s
所以在这段时间内B所通过的位移的大小为
x=
| v0+v1 |
| 2 |
| v1+v2 |
| 2 |
| v2+v3 |
| 2 |
答:(1)物块P从开始自由下落到再次回到初始位置所经历的时间是4.08s;
(2)在这段时间内B所通过的位移的大小为36m.
点评:本题考查运用牛顿第二定律和运动学公式分析和解决复杂动力学问题的能力,关键是分析受力情况和运动情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,P为位于某一高度处的质量为m的物块,B为位于水平地面上的质量为M的特殊长平板,m/M=1/10,平板与地面间的动摩擦因数为μ=2.00×10-2.在板的上表面上方,存在一定厚度的“相互作用区域”,如图中划虚线的部分,当物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=α mg,α=51,f对P的作用使P刚好不与B的上表面接触;在水平方向P、B之间没有相互作用力.已知物块P开始自由落下的时刻,板B向右的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2s.设B板足够长,保证物块P总能落入B板上方的相互作用区,取重力加速度g=9.8m/s2.问:当B开始停止运动那一时刻,P已经回到过初始位置几次?
如图所示,P为位于某一高度处的质量为m的物块,B为位于水平地面上的质量为M的特殊长平板,m/M=1/10,平板与地面间的动摩擦因数为μ=2.00×10-2.在板的上表面上方,存在一定厚度的“相互作用区域”,如图中划虚线的部分,当物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=α mg,α=51,f对P的作用使P刚好不与B的上表面接触;在水平方向P、B之间没有相互作用力.已知物块P开始自由落下的时刻,板B向右的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2s.设B板足够长,保证物块P总能落入B板上方的相互作用区,取重力加速度g=9.8m/s2.问:当B开始停止运动那一时刻,P已经回到过初始位置几次?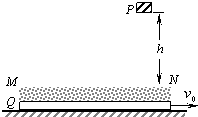 (2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,
(2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,