题目内容
如图所示，P为位于某一高度处的质量为m的物块，B为位于水平地面上的质量为M的特殊长平板，m/M=1/10，平板与地面间的动摩擦因数为μ=2.00×10-2．在板的上表面上方，存在一定厚度的“相互作用区域”，如图中划虚线的部分，当物块P进入相互作用区时，B便有竖直向上的恒力f作用于P，f=α mg，α=51，f对P的作用使P刚好不与B的上表面接触；在水平方向P、B之间没有相互作用力．已知物块P开始自由落下的时刻，板B向右的速度为v0=10m/s．P从开始下落到刚到达相互作用区所经历的时间为T0=2s．设B板足够长，保证物块P总能落入B板上方的相互作用区，取重力加速度g=9.8m/s2．问：当B开始停止运动那一时刻，P已经回到过初始位置几次？分析：P物体的运动具有周期性，根据牛顿第二定律和运动学公式算出一个周期的时间；然后根据牛顿第二定律和运动学公式求解出在A运动的一个周期内B的速度减小量；最后得到B的运动总时间．
解答：解：当P进入相互作用区前，P作自由落体运动，V=gT0=19.8m/s
B受摩擦力f1=μMg作用作减速运动，f1=Ma1 所以a1=μg
当P进入相互作用区后，P作匀减速后反向匀加速运动，
f-mg=ma 所以a=（α-1）g=50g=490m/s2 则t2=
=0.04s
B受摩擦力f2=μ（αmg+Mg）作用作减速运动，
f2=Ma2 所以a2=μg+
μg
可见：当P下落又返回的一个周期内，B的速度减小为：
△V=a1×2T0+a2×2t2
则B停止运动前P返回的次数为：n=
=20.5，即20次
答：当B开始停止运动那一时刻，P已经回到过初始位置20次．
B受摩擦力f1=μMg作用作减速运动，f1=Ma1 所以a1=μg
当P进入相互作用区后，P作匀减速后反向匀加速运动，
f-mg=ma 所以a=（α-1）g=50g=490m/s2 则t2=
| v |
| a |
B受摩擦力f2=μ（αmg+Mg）作用作减速运动，
f2=Ma2 所以a2=μg+
| αm |
| M |
可见：当P下落又返回的一个周期内，B的速度减小为：
△V=a1×2T0+a2×2t2
则B停止运动前P返回的次数为：n=
| V0 |
| △v |
答：当B开始停止运动那一时刻，P已经回到过初始位置20次．
点评：本题关键找出物体A运动的周期性，确定一个周期内物体A的运动规律，得到A的运动的周期，同时求解出在一个周期内B物体的速度改变量，不难．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图所示，P为位于某一高度处的质量为m的小物块（可视为质点），B为位于水平地面上的质量为M的特殊长平板，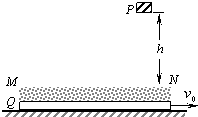
（2005?福建模拟）如图所示，P为位于某一高度处的质量为m的物块，Q为位于水平地面上的质量为M的特殊平板，