题目内容
 如图所示,P为位于某一高度处的质量为m的物块,B为位于水平地面上的质量为M的特殊长平板,
如图所示,P为位于某一高度处的质量为m的物块,B为位于水平地面上的质量为M的特殊长平板,| m |
| M |
| 1 |
| 10 |
(1)物块P从开始自由下落到再次回到初始位置所经历的时间;
(2)当B开始停止运动的那一时刻,P已经回到初始位置多少次.
分析:(1)根据自由落体运动的公式求出物体P进入相互作用区域时的速度大小,结合牛顿第二定律求出进入相互作用区域的加速度,通过运动学公式,抓住运动的对称性求出物块P从开始下落到再次回到初始位置所经历的时间.
(2)根据动量定律求出在一个周期内动量的变化量,得出速度的变化量,从而通过整个过程中速度的变化量求出物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数.
(2)根据动量定律求出在一个周期内动量的变化量,得出速度的变化量,从而通过整个过程中速度的变化量求出物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数.
解答:解:(1)物块P进入相互作用区域时的速度为V1,则
v1=gt0=20m/s
物块P从进入相互作用区域到速度减小为零的过程中,受到重力和平板的相互作用,设物块在相互作用区域内的下落的加速度为a,根据牛顿第二定律:
kmg-mg=ma
设在相互作用区域内的下落时间为t,根据运动学公式t=
而物块从开始下落到回到初始位置的时间T=2(t+t0)=
t0=4.4s
(2)设在一个运动的周期T内,平板B的速度减小量为△v,根据动量定理有
μMg?2t0+μ(Mg+f)?2t=M△v
解得△v=2μgt0+2μg(1+
)?
t0
P回到初始位置的次数n=
=10.3
n应取整数,即n=10.
答:(1)物块P从开始下落到再次回到初始位置所经历的时间为4.4s.
(2)从物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数为10.
v1=gt0=20m/s
物块P从进入相互作用区域到速度减小为零的过程中,受到重力和平板的相互作用,设物块在相互作用区域内的下落的加速度为a,根据牛顿第二定律:
kmg-mg=ma
设在相互作用区域内的下落时间为t,根据运动学公式t=
| v1 |
| a |
而物块从开始下落到回到初始位置的时间T=2(t+t0)=
| 2k |
| k+1 |
(2)设在一个运动的周期T内,平板B的速度减小量为△v,根据动量定理有
μMg?2t0+μ(Mg+f)?2t=M△v
解得△v=2μgt0+2μg(1+
| km |
| M |
| 1 |
| k-1 |
P回到初始位置的次数n=
| v0 |
| △v |
n应取整数,即n=10.
答:(1)物块P从开始下落到再次回到初始位置所经历的时间为4.4s.
(2)从物块P开始下落到平板B的运动速度减小为零的这段时间内,P能回到初始位置的次数为10.
点评:本题综合考查了动量定理、牛顿第二定律、运动学公式等,综合性较强,难度中等,需加强这类题型的训练.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图所示,P为位于某一高度处的质量为m的小物块(可视为质点),B为位于水平地面上的质量为M的特殊长平板,
如图所示,P为位于某一高度处的质量为m的小物块(可视为质点),B为位于水平地面上的质量为M的特殊长平板,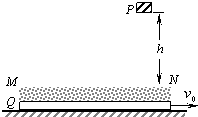 (2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,
(2005?福建模拟)如图所示,P为位于某一高度处的质量为m的物块,Q为位于水平地面上的质量为M的特殊平板,