题目内容
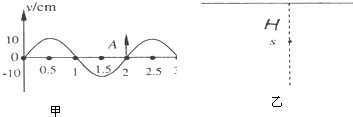
(1)如图甲所示,一列简谐波沿x轴传播,实线为t=0时的波形图,此时P质点向y轴负方向运动,虚线为经过0.01s时第一次出现的波形图,则波沿x轴 (填“正”或“负”)方向传播,波速为 m/s.
(2)某同学欲测直角三棱镜ABC的折射率n.他让光线沿平行于BC边的方向射到三棱镜的侧面AB上,经棱镜AB边和AC边的两次折射和BC边的一次反射后,又从另一侧面AC边上的P点射出.
①在图乙上画出光路图;
②若将射向AB边的光的入射角调整为α=60°,此时的折射角γ=30°,求折射率n的值.
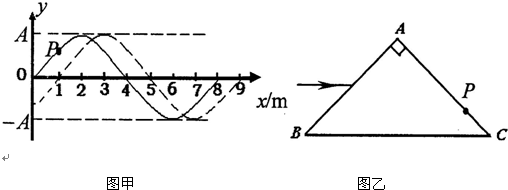
(2)某同学欲测直角三棱镜ABC的折射率n.他让光线沿平行于BC边的方向射到三棱镜的侧面AB上,经棱镜AB边和AC边的两次折射和BC边的一次反射后,又从另一侧面AC边上的P点射出.
①在图乙上画出光路图;
②若将射向AB边的光的入射角调整为α=60°,此时的折射角γ=30°,求折射率n的值.

分析:(1)由题,此时P质点向y轴负方向运动,判断出波传播方向,根据波形的平移法和周期性得到波传播△x的距离通项,由公式v=
求出波速.
(2)①光线经过棱镜两次折射后从AC侧面射出时,在BC面上发生了全反射,画出光路图.在AC面上和AB面上,分别运用折射定律列式;
②根据几何关系得到AC面上折射角与AB面上入射角之间的关系,联立即可求得n.
| △x |
| △t |
(2)①光线经过棱镜两次折射后从AC侧面射出时,在BC面上发生了全反射,画出光路图.在AC面上和AB面上,分别运用折射定律列式;
②根据几何关系得到AC面上折射角与AB面上入射角之间的关系,联立即可求得n.
解答: 解:(1)由题,此时P质点向y轴负方向运动,根据波形平移法判断出波沿x轴正方向传播.
解:(1)由题,此时P质点向y轴负方向运动,根据波形平移法判断出波沿x轴正方向传播.
根据波的周期性可知,波传播的距离为△x=(nλ+1)m=(8n+1)m,n=0,1,2,…
则波速为 v=
=
m/s=100(8n+1)m/s,n=0,1,2,…
(2))①由题意知:光线在BC面上发生了全反射,画出光路图如图所示.
②根据反射定律和几何关系知:光线在AB面的折射角为γ=30°,
则折射率为 n=
=
故答案为:(1)正; 100(8n+1)m/s,n=0,1,2,…;
(2)①光路图如图所示.②折射率n的值为
.
 解:(1)由题,此时P质点向y轴负方向运动,根据波形平移法判断出波沿x轴正方向传播.
解:(1)由题,此时P质点向y轴负方向运动,根据波形平移法判断出波沿x轴正方向传播.根据波的周期性可知,波传播的距离为△x=(nλ+1)m=(8n+1)m,n=0,1,2,…
则波速为 v=
| △x |
| △t |
| 8n+1 |
| 0.01 |
(2))①由题意知:光线在BC面上发生了全反射,画出光路图如图所示.
②根据反射定律和几何关系知:光线在AB面的折射角为γ=30°,
则折射率为 n=
| sinα |
| siny |
| 3 |
故答案为:(1)正; 100(8n+1)m/s,n=0,1,2,…;
(2)①光路图如图所示.②折射率n的值为
| 3 |
点评:第1题要抓住波的周期性,得到波传播距离的通项是关键;第2题关键要判断出光线在BC面上发生了全反射,运用几何关系求解AB面上的折射角.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目

 (1)如图甲所示为一拉力传感器,某实验小组在用拉力传感器探究作用力与反作用力关系的实验中,获得了如图乙所示的图线.根据这个图线,你可以得出的结论是:
(1)如图甲所示为一拉力传感器,某实验小组在用拉力传感器探究作用力与反作用力关系的实验中,获得了如图乙所示的图线.根据这个图线,你可以得出的结论是: 两同学分别用不同的方法测定一半圆柱形玻璃砖的折射率.
两同学分别用不同的方法测定一半圆柱形玻璃砖的折射率.