题目内容
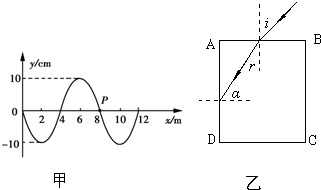
(1)如图甲所示是一列横波在某一时刻的波形图象,已知这列波的频率为4Hz,A点在此时的振动方向如图所示.则可以判断出这列波的传播方向是沿x 轴 方向(填“正”或“负”),波速大小为 m/s
(2)如图乙所示,在平静的水面下有一点光源s,点光源到水面的距离为H,水对该光源发出的单色光的折射率为n.请解答下列问题:
①在水面上方可以看到一圆形的透光面,求该圆的半径.
②若该单色光在真空中的波长为λ0,该光在水中的波长为多少?
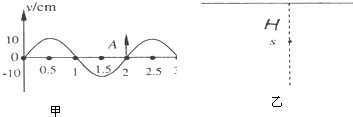
(2)如图乙所示,在平静的水面下有一点光源s,点光源到水面的距离为H,水对该光源发出的单色光的折射率为n.请解答下列问题:
①在水面上方可以看到一圆形的透光面,求该圆的半径.
②若该单色光在真空中的波长为λ0,该光在水中的波长为多少?

分析:本题(1)的关键是根据波的传播方向与质点振动方向间的关系判定波的传播方向(可以用“上坡向下,下坡向上”来形象记忆.(2)题的关键是画出光的全反射图,然后根据折射定律及几何知识即可求出圆的半径;再根据光在传播过程中频率不变,利用波速、波长与频率的关系即可求出光在水中的波长.
解答:解:(1)根据波的传播方向与质点振动方向间的关系可知,由于质点2的振动方向向上,所以波向x轴的负向传播,
由图象读出λ=2m,所以波速v=fλ=4×2m/s=8m/s.
故答案为:负,8
(2)①做出全反射光路图如图,设光在水面发生全反射的临界角为C,应有sinC=
=
,解得r=
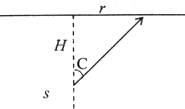
故该圆的半径为r=
②由于光在传播过程中的频率不变,设光在真空中的传播速度为c,在水中的传播速度为v,应有n=
,又f=
=
联立解得λ=
故该光在水中的波长为λ=
由图象读出λ=2m,所以波速v=fλ=4×2m/s=8m/s.
故答案为:负,8
(2)①做出全反射光路图如图,设光在水面发生全反射的临界角为C,应有sinC=
| r | ||||||
|
| 1 |
| n |
| H | ||||
|

故该圆的半径为r=
| H | ||||
|
②由于光在传播过程中的频率不变,设光在真空中的传播速度为c,在水中的传播速度为v,应有n=
| c |
| v |
| c | ||
|
| v |
| λ |
联立解得λ=
| ||
| n |
故该光在水中的波长为λ=
| ||
| n |
点评:对波的图象问题,可以通过“爬坡法”形象记忆质点振动方向与波传播方向间的关系;对有关全反射问题,关键是画出光路图,然后根据折射定律列式求解;要熟记光在不同介质中的频率不变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
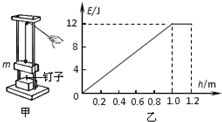 如图甲所示是一打桩机的简易模型.质量m=1kg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击钉子,将钉子打入一定深度.物体上升过程中,机械能E与上升高度h的关系图象如图乙所示.不计所有摩擦,g取10m/s2.( )
如图甲所示是一打桩机的简易模型.质量m=1kg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击钉子,将钉子打入一定深度.物体上升过程中,机械能E与上升高度h的关系图象如图乙所示.不计所有摩擦,g取10m/s2.( )| A、拉力F的大小为12N | B、物体上升1.0m处的速度为2m/s | C、撤去F后物体上升时间为0.1s | D、物体上升到0.25m高度处拉力F的瞬时功率12W |