题目内容
3．如图所示，在国庆阅兵演习中，某直升飞机在地面上空某高度A位置处于静止状态待命，接上级命令，要求该机10时58分由静止状态沿水平方向做匀加速直线运动，10时58分50秒到达B位置，然后就进入BC段的匀速受阅区，10时59分40秒准时通过C位置，已知BC段的距离xBC=10km．问：
（1）直升飞机在BC段的速度大小是多少？
（2）直升飞机在AB段做匀加速直线运动时的加速度大小是多少？
分析 （1）根据匀速直线运动的位移和时间求出直升飞机在BC段的速度大小．
（2）根据速度时间公式求出直升飞机在AB段做匀加速直线运动时的加速度大小．
解答 解：（1）BC段运行的时间t2=50s，
则直升飞机在BC段的速度大小为：v=$\frac{{x}_{BC}}{{t}_{2}}=\frac{10000}{50}m/s=200m/s$．
（2）直升飞机在AB段的加速度大小为：a=$\frac{v}{{t}_{1}}=\frac{200}{50}m/{s}^{2}=4m/{s}^{2}$．
答：（1）直升飞机在BC段的速度大小是200m/s；
（2）直升飞机在AB段做匀加速直线运动时的加速度大小是4m/s2．
点评 解决本题的关键掌握匀变速直线运动的速度时间公式，结合匀速运动的位移公式求出B点的速度是解决本题的突破口．
练习册系列答案
阅读快车系列答案
相关题目
18．在平直道路上，甲汽车以速度v匀速行驶．当甲车司机发现前方距离为d处的乙汽车时，立即以大小为a1的加速度匀减速行驶，与此同时，乙车司机也发现了甲，立即从静止开始以大小为a2的加速度沿甲车运动的方向匀加速运动．则 （ ）
| A． | 甲、乙两车之间的距离一定不断减小 | |
| B． | 甲、乙两车之间的距离一定不断增大 | |
| C． | 若v＞$\sqrt{2{a}_{1}+{a}_{2}d}$，则两车一定不会相撞 | |
| D． | 若v＜$\sqrt{2（{a}_{1}+{a}_{2}）d}$，则两车一定不会相撞 |
15．
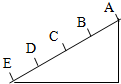如图所示，光滑斜面AE被分成四个相等的部分，一物体由A点从静止释放，沿着斜面做匀加速直线运动，下列结论中正确的是（ ）
如图所示，光滑斜面AE被分成四个相等的部分，一物体由A点从静止释放，沿着斜面做匀加速直线运动，下列结论中正确的是（ ）| A． | 各段的速度增加量相等 | |
| B． | 各段位移所用的时间之比为tAB：tBC：tCD：tDE=1：$\sqrt{2}$：$\sqrt{3}$：2 | |
| C． | 物体从A到E的平均速度$\overline{v}$AE=vB | |
| D． | 物体在C点的速度vC=$\sqrt{\frac{{v}_{B}^{2}+{v}_{D}^{2}}{2}}$且vC＞$\frac{{v}_{B}+{v}_{D}}{2}$ |
12．一物体运动的位移与时间关系x=24t-3t2（m）（t以s为单位）则（ ）
| A． | 这个物体做匀变速运动 | B． | 这个物体的初速度为24m/s | ||
| C． | 这个物体加速度为6m/s2 | D． | 4s末物体离出发点距离为48m |