题目内容
8.现一辆摩托车和一自行车沿同一平直公路同向运动.开始时,自行车在摩托车的前方s0=27m处.自行车始终以v1=6m/s的速度匀速运动.摩托车初速度为零,加速度为2m/s2的匀加速直线运动.求:(1)摩托车追上自行车之前,两车之间的最大距离s
(2)经过多长时间,摩托车追上自行车?
(3)摩托车一追上自行车,摩托车就立即刹车,减速过程加速度大小为a=2m/s2,则再经过多少时间,两车再次相遇.(设摩托车在自行车旁通过,不发生相撞)
分析 (1)当两车速度相等时,有最大距离,结合速度时间公式求出两车速度相等经历的时间,根据位移公式求出两车之间的最大距离.
(2)根据位移关系,结合运动学公式求出追及的时间.
(3)根据速度时间公式求出摩托车追上自行车的速度,根据位移关系,求出再次相遇的时间.
解答 解:(1)当两车速度相等时,有最大距离,则速度相等经历的时间为:
${t}_{1}=\frac{{v}_{1}}{a}=\frac{6}{2}s=3s$,
则相距的最大距离为:
$△x={v}_{1}{t}_{1}+{s}_{0}-\frac{1}{2}a{{t}_{1}}^{2}$=$6×3+27-\frac{1}{2}×2×9m$=36m.
(2)根据位移关系有:${v}_{1}t+{s}_{0}=\frac{1}{2}a{t}^{2}$,
代入数据解得:t=9s.
(3)摩托车追上自行车时,速度为:v0=at=2×9m/s=18m/s,
设经过t′时间两车再次相遇,有:${v}_{0}t′-\frac{1}{2}at{′}^{2}={v}_{1}t′$,
代入数据解得t′=12s,
因为摩托车速度减为零的时间为:${t}_{0}=\frac{0-{v}_{0}}{a}=\frac{-18}{-2}s=9s$,知再次相遇前摩托车已经停止,
摩托车匀减速运动的位移为:$x′=\frac{{{v}_{0}}^{2}}{2a}=\frac{1{8}^{2}}{4}m=81m$,
则再次相遇的时间为:$t″=\frac{x′}{{v}_{1}}=\frac{81}{6}s=13.5s$.
答:(1)摩托车追上自行车之前,两车之间的最大距离为36m;
(2)经过9s时间,摩托车追上自行车.
(3)再经过13.5s时间,两车再次相遇.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时相距最远,对于第三问,要注意摩托车速度减为零的时间.

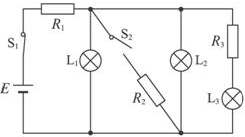
| A. | 电源输出功率减小 | B. | L1上消耗的功率增大 | ||
| C. | 通过R1上的电流增大 | D. | 通过R3上的电流增大 |
 在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )
在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )| A. | φb>φa=φc>φo | |
| B. | φo>φa>φb>φc | |
| C. | 将质子从a点移到c点,电场力做功大于eE0d | |
| D. | 将质子由a点移到c点,质子的电势能增加 |
| A. | 物体经过AB位移中点的速度大小为7m/s | |
| B. | 物体经过AB位移中点的速度大小为7.07m/s | |
| C. | 物体通过AB这段位移的平均速度为7m/s | |
| D. | 物体通过AB这段位移所用时间的中间时刻的速度为5m/s |
| A. | 相等时间间隔内的位移之差为常数 | |
| B. | 任意两个相等时间内的速度变化量都相等 | |
| C. | 从开始运动起,在连续相等时间内通过的位移之比为1:4:9:… | |
| D. | 从开始运动起,通过连续相等的位移所需的时间之比为1:3:5:… |
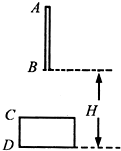 如图所示,一直杆AB长l=3.8m,直杆的下端B距窗台D高度H=6m,CD是高为d=1m的窗口,直杆从图示位置由静止开始自由下落,求:
如图所示,一直杆AB长l=3.8m,直杆的下端B距窗台D高度H=6m,CD是高为d=1m的窗口,直杆从图示位置由静止开始自由下落,求: 如图所示,两用力推一辆熄火的汽车,每人用力的大小都是500N,方向都在水平面内且跟车的运动方向成30°角,则在推车过程中两人的合力是$500\sqrt{3}$N(cos30°=0.866,sin30°=0.5)
如图所示,两用力推一辆熄火的汽车,每人用力的大小都是500N,方向都在水平面内且跟车的运动方向成30°角,则在推车过程中两人的合力是$500\sqrt{3}$N(cos30°=0.866,sin30°=0.5)