题目内容
（19分）如图所示，AB为半径R=0.8m的1/4光滑圆弧轨道，下端B恰与小车右端平滑对接。小车质量M=3kg，车长L=2.06m，车上表面距地面的高度h=0.2m。现有一质量m=1kg的滑块，由轨道顶端无初速度释放，滑到B端后冲上小车。已知地面光滑，滑块与小车上表面间的动摩擦因数
=0.3，当车运行了1.5 s时，被地面装置锁定(g=10m/s2)。求：
（1）滑块到达B端时，轨道对它支持力的大小；
（2）车被锁定时，车右端距轨道B端的距离；
（3）从车开始运动到被锁定的过程中，滑块与车面间由于摩擦而产生的内能大小；
（4）滑块落地点离车左端的水平距离。
=0.3，当车运行了1.5 s时，被地面装置锁定(g=10m/s2)。求：（1）滑块到达B端时，轨道对它支持力的大小；
（2）车被锁定时，车右端距轨道B端的距离；
（3）从车开始运动到被锁定的过程中，滑块与车面间由于摩擦而产生的内能大小；
（4）滑块落地点离车左端的水平距离。
(1) 30N , (2) 1m , (3) 6J , (4) 0.16m 。
试题分析：（1）设滑块到达B端时的速度为
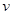，由动能定理得：
由牛顿第二定律得：
，联立两式解得
。（2）当滑块滑上小车后，由牛顿第二定律对滑块有
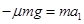；对小车有：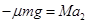
设经过时间
两者达到共同速度，则有：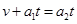
，解得：
，由于
，此时小车还未被锁定，两者的共同速度：
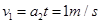。因此，车陂锁定时，车右端距轨道B的距离
（3）从车开始运动到被锁定的过程中，滑块相对小车滑动的距离
，所以产生的内能：
（4）对滑块由动能定理得：
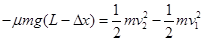
滑块脱离小车后，在竖直方向有：
则，滑块落地点离车左端的水平距离：
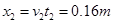
练习册系列答案
特高级教师点拨系列答案
相关题目
，高
，质量为
的平顶车，车顶面光滑，在牵引力为零时，仍在向前运动，设车运动时受到的阻力与它对地面的压力成正比，且比例系数
。当车速为
时，把一个质量为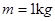
的物块（视为质点）轻轻放在车顶的前端，并开始计时。那么，经过t= s物块离开平顶车；物块落地时，落地点距车前端的距离为s= m。（取
）
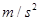的加速度做匀减速直线运动，且着陆速度为60
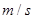，求：
内飞机滑行的距离；