题目内容
 (选修3-4模块)
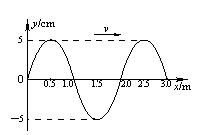
(选修3-4模块)如图的实线是某时刻的波形图象,虚线是经过△t=0.2s时的波形图象.
(1)假定波向左传播,求它传播的可能距离.
(2)若这列波向右传播,周期T和△t满足2T>△t>T,求波的传播速度.
(3)假定波速是70m/s,求波的传播方向.
分析:(1)由图波长λ=4m.波向左传播的最短距离为3m,即
λ,根据波的周期性:波经过整数倍时间,图形相同,求出波传播的距离.
(2)若这列波向右传播时,周期T和△t满足2T>△t>T,根据周期与时间关系的通项求出周期.读出波长,由波速公式求波速.
(3)根据波速是70m/s和时间0.2s求出波传播的距离,分析与波长的关系,根据波形的平移,确定波的传播方向.
| 3 |
| 4 |
(2)若这列波向右传播时,周期T和△t满足2T>△t>T,根据周期与时间关系的通项求出周期.读出波长,由波速公式求波速.
(3)根据波速是70m/s和时间0.2s求出波传播的距离,分析与波长的关系,根据波形的平移,确定波的传播方向.
解答:解:(1)由图知:波长λ=8m
波向左传播时的距离为 s=(n+
)λ=8(n+
)=(8n+6)m,(n=0、1、2…)可能值有6m、14m、22m…
(2)根据△t=(n+
)T 且2T>△t>T,
故n=1,T=
△t=0.8×0.2s=0.16s,
则波速v=
=
m/s=50m/s
(3)波在0.2s传播的距离,s=vt=70×0.2m=14m,
因
=
=1
,即s=1
λ=λ+
λ
则结合波形图知,波向左传播.
答:
(1)假定波向左传播,它传播的可能距离是(8n+6)m,(n=0、1、2…).
(2)若这列波向右传播,周期T和△t满足2T>△t>T,波的传播速度是50m/s.
(3)假定波速是70m/s,波的传播方向向左.
波向左传播时的距离为 s=(n+
| 3 |
| 4 |
| 3 |
| 4 |
(2)根据△t=(n+
| 1 |
| 4 |
故n=1,T=
| 4 |
| 5 |
则波速v=
| λ |
| T |
| 8 |
| 0.16 |
(3)波在0.2s传播的距离,s=vt=70×0.2m=14m,
因
| s |
| λ |
| 14 |
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
则结合波形图知,波向左传播.
答:
(1)假定波向左传播,它传播的可能距离是(8n+6)m,(n=0、1、2…).
(2)若这列波向右传播,周期T和△t满足2T>△t>T,波的传播速度是50m/s.
(3)假定波速是70m/s,波的传播方向向左.
点评:本题考查理解波动图象的能力以及运用数学通项求解特殊值的能力.对于两个时刻的波形,有时还要考虑波的双向性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目