��Ŀ����
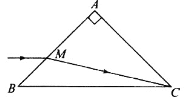
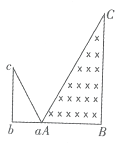
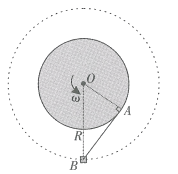
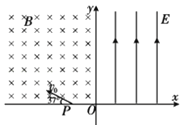
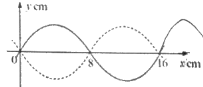
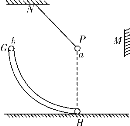
����Ŀ����ͼ��ʾ�������뾶��ͬ�İ�Բ�ι���ֱ���ֱ������ǿ�糡����ǿ�ų��У����������ͬһ�߶��ϣ�����ǹ⻬�ģ�������ͬ�Ĵ�����С��ͬ�������������ߵ��ɾ�ֹ�ͷţ�M��NΪ�������͵㣬������
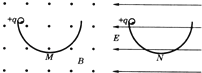
A. ��С������͵���ٶ�vM��vN
B. ��С������͵�ʱ�Թ����ѹ��FM��FN
C. С���һ�ε���M���ʱ�����С���һ�ε���N���ʱ��
D. �ڴų���С���ܵ���������һ�ˣ��ڵ糡��С���ܵ���������һ��
���𰸡�BD
��������
��������İ뾶��ͬ������Բ���˶����������Ĺ�ʽ���Է���С��ͨ����͵��ǶԹ����ѹ����С���ڴų����˶����ų�����С������������������С��Ļ�е���غ㣬С���ڵ糡���ܵ��ĵ糡����С����������������͵�ʱ���ٶȵĴ�С��С��
С���ڴų����˶�������͵��������������֪��
![]()
��ã�![]() ����
����
С���ڵ糡���˶�������͵�����������֪��![]()
��ã�![]() ����
����
A��C������С���ڴų����˶����ų�����С������������������С��Ļ�е���غ㣻��С���ڵ糡���˶��ܵ��ĵ糡����С����������������͵�ʱ���ٶȵĴ�С��С��������������͵���ٶȴ�С���ȣ����ڵ糡���˶���ʱ��Ҳ������AC����
B����Ϊv1��v2����Ϣ٢ڿ�֪��FM��FN����B��ȷ��
D������С���ڴų����˶����ų�����С������������������С��Ļ�е���غ㣬����С����Ե���������һ�ˣ����糡����С��������������С���ڴﵽ�����һ��֮ǰ�ٶȾͼ�Ϊ���ˣ��ʲ��ܵ������Ҷˣ���D��ȷ��
��ѡ��BD��