题目内容
19.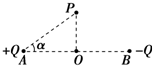 如图所示,相距为2d的A和B两点上固定着等量异种的两个点电荷,电荷量分别为+Q和-Q.在AB连线的中垂线上取一点P,垂足为O,∠PAO=α,求:
如图所示,相距为2d的A和B两点上固定着等量异种的两个点电荷,电荷量分别为+Q和-Q.在AB连线的中垂线上取一点P,垂足为O,∠PAO=α,求:(1)P点的场强的大小和方向.
(2)α为何值时,场强最大,其最大值是多少?
分析 先利用几何关系求出AP间的距离,再利用点电荷的场强公式和场强叠加即可求出P的场强;然后利用数学求极值即可求解.
解答 解析:(1)如图所示,P点场强是正、负电荷在P点产生场强的矢量和.
由E=k$\frac{Q}{r2}$得
EP=2Ecosα=α$\frac{2kQ}{{d}^{2}}co{s}^{3}α$,方向向右.
(2)由上式表明
当α=0时,得:
EP(max)=$\frac{2kQ}{d2}$,方向向右.
答:(1)P点的场强大小$\frac{2kQ}{d2}$cos3α,方向向右 (2)当α=0时,P点的场强最大$\frac{2kQ}{d2}$,方向向右
点评 此题思路较简单,是点电荷的场强公式和场强的叠加,但要注意用三角函数找几何关系,基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.关于重力和重心的以下说法,你认为正确的是( )
| A. | 重力就是地球对物体的吸引力 | |
| B. | 重力是由于地球的吸引而使物体受到的力 | |
| C. | 物体的重心位置与物体的质量分布情况和物体的形状有关 | |
| D. | 物体的重心一定在物体的几何中心上 |
14.某实验小组为描绘“4V 2W”的小灯泡的U-I特性曲线,除导线和开关外,实验室还有以下器材可供选择:
电流表 (量程为0.6A,内阻约为1Ω)
(量程为0.6A,内阻约为1Ω)
电流表 (量程为3.0A,内阻约为0.2Ω)
(量程为3.0A,内阻约为0.2Ω)
电压表 (量程为5.0V,内阻约为5kΩ)
(量程为5.0V,内阻约为5kΩ)
电压表 (量程为15.0V,内阻约为15kΩ)
(量程为15.0V,内阻约为15kΩ)
滑动变阻器R1(最大电阻为200Ω,额定电流100mA)
滑动变阻器R2(最大电阻为10Ω,额定电流1.0A)
电源(电动势为6.0V,内阻约为1.5Ω)
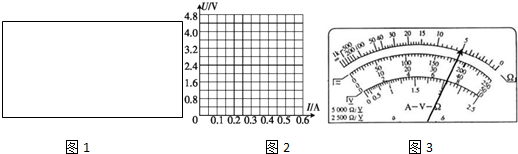
(ⅰ)为了使实验结果尽可能的准确,请画出该实验合理的电路图如图1(在电路图中标出所选仪器的字母符号).
(ⅱ)经过正确的操作,测得的数据如表,请根据下表中的数据在坐标系中描点,然后画出如图2灯泡的U-I曲线.(只描9、10、11三点)
(ⅲ)如图3示是一位同学利用万用电表(×1挡)测量该小灯泡的电阻时指针所示的位置,该示数为5.0Ω.接在电路中进行测量时,当小灯泡两端的电压为1.20V时,小灯泡的电阻约为4.0Ω.
电流表
 (量程为0.6A,内阻约为1Ω)
(量程为0.6A,内阻约为1Ω)电流表
 (量程为3.0A,内阻约为0.2Ω)
(量程为3.0A,内阻约为0.2Ω)电压表
 (量程为5.0V,内阻约为5kΩ)
(量程为5.0V,内阻约为5kΩ)电压表
 (量程为15.0V,内阻约为15kΩ)
(量程为15.0V,内阻约为15kΩ)滑动变阻器R1(最大电阻为200Ω,额定电流100mA)
滑动变阻器R2(最大电阻为10Ω,额定电流1.0A)
电源(电动势为6.0V,内阻约为1.5Ω)

(ⅰ)为了使实验结果尽可能的准确,请画出该实验合理的电路图如图1(在电路图中标出所选仪器的字母符号).
(ⅱ)经过正确的操作,测得的数据如表,请根据下表中的数据在坐标系中描点,然后画出如图2灯泡的U-I曲线.(只描9、10、11三点)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| U/V | 0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 | 3.60 | 4.00 |
| I/A | 0 | 0.12 | 0.22 | 0.30 | 0.36 | 0.40 | 0.43 | 0.46 | 0.48 | 0.49 | 0.50 |
4.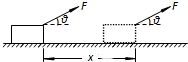 如图所示,一个物块在与水平方向成θ角的拉力F作用下,沿水平面向右运动一段距离x.在此过程中,拉力F对物块做的功为( )
如图所示,一个物块在与水平方向成θ角的拉力F作用下,沿水平面向右运动一段距离x.在此过程中,拉力F对物块做的功为( )
 如图所示,一个物块在与水平方向成θ角的拉力F作用下,沿水平面向右运动一段距离x.在此过程中,拉力F对物块做的功为( )
如图所示,一个物块在与水平方向成θ角的拉力F作用下,沿水平面向右运动一段距离x.在此过程中,拉力F对物块做的功为( )| A. | Fx | B. | Fxsinθ | C. | Fxcosθ | D. | Fxtanθ |
11. 如图,a、b、c、d是四根长度相等、等间距地被固定在同一竖直平面上的通电长直导线,当它们通以大小相等、方向如图的电流时,各导线所受磁场力的合力情况是( )
如图,a、b、c、d是四根长度相等、等间距地被固定在同一竖直平面上的通电长直导线,当它们通以大小相等、方向如图的电流时,各导线所受磁场力的合力情况是( )
 如图,a、b、c、d是四根长度相等、等间距地被固定在同一竖直平面上的通电长直导线,当它们通以大小相等、方向如图的电流时,各导线所受磁场力的合力情况是( )
如图,a、b、c、d是四根长度相等、等间距地被固定在同一竖直平面上的通电长直导线,当它们通以大小相等、方向如图的电流时,各导线所受磁场力的合力情况是( )| A. | 导线a的受力方向向右 | B. | 导线b的受力方向向左 | ||
| C. | 导线c的受力方向向左 | D. | 导线d的受力方向向右 |
8.某发电厂原来用22KV的交流电压输电,后来改用升压变压器将电压升高到220KV输电,两次输送的电功率相同,下列说法正确的是( )
| A. | 提高电压后输电线上的电流降为原来的$\frac{1}{10}$ | |
| B. | 提高电压后输电线上的电流变为原来的10倍 | |
| C. | 提高电压后输电线上损失的电压变为原来的10倍 | |
| D. | 提高电压后输电线上的功率损耗降为原来的$\frac{1}{10}$ |
9. 如图所示.场强方向竖直向下的匀强电场中,有三个质量相等,分别带正电、负电和不带电的质点,由两水平极板正中,以相同的初速度(V0),先后垂直射入电场,并分别落在负极板上甲、乙、丙三处,可以判定( )
如图所示.场强方向竖直向下的匀强电场中,有三个质量相等,分别带正电、负电和不带电的质点,由两水平极板正中,以相同的初速度(V0),先后垂直射入电场,并分别落在负极板上甲、乙、丙三处,可以判定( )
 如图所示.场强方向竖直向下的匀强电场中,有三个质量相等,分别带正电、负电和不带电的质点,由两水平极板正中,以相同的初速度(V0),先后垂直射入电场,并分别落在负极板上甲、乙、丙三处,可以判定( )
如图所示.场强方向竖直向下的匀强电场中,有三个质量相等,分别带正电、负电和不带电的质点,由两水平极板正中,以相同的初速度(V0),先后垂直射入电场,并分别落在负极板上甲、乙、丙三处,可以判定( )| A. | 甲处质点带正电,乙处质点不带电,丙处质点带负电 | |
| B. | 三个质点在电场中的运动时间相等 | |
| C. | 三个质点在电场中的加速度a甲>a乙>a丙 | |
| D. | 三个质点到达负极的动能EK甲>EK乙>EK丙 |