��Ŀ����
��ͼ��ʾ�������ֱ������ϵXOY���ڵ�һ�������д�ֱֽ���������ǿ�ų����ڵ����������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȵĴ�С��ΪB���ڵڶ�����������x���������ǿ�糡��������������һ��ƽ�н�����M��N��������Ϊd�����ӵ�ѹΪU��������д�ֱֽ������Ÿ�Ӧǿ��ΪB0����ǿ�ų���һ����������ƽ���ڽ������������������䲢��ֱ���˶�����A�㣨��L��0����ֱ��x�����ڶ����ޣ���P��0��2L�������һ���ޣ�Ȼ�����Ӵ�ֱ��x���뿪��һ���ޣ��������ӵ���������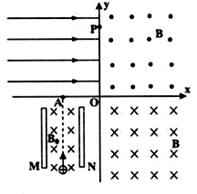
��1�������ڽ�������˶��ٶ�V0�Ĵ�С
��2�����ӵıȺ�q/m
��3�������ӽ����һ����ʼ��ʱ�����Ӵ�Խx���ʱ��
��1�� ��2��
��2�� ��3��
��3�� n��(0,1,2,����)
n��(0,1,2,����)
�������������(1)�����ڰ����ֱ���˶����糡������������ƽ��
qE=qv0B0 

(2)�����ڵڶ�����������ƽ���˶���������P��ʱ��y�᷽��ķ��ٶ�Ϊv0������x����ķ��ٶ�Ϊvx
2L=v0t ��L= vxt ��vx=v0
vxt ��vx=v0
������P��ʱ���ٶ���y���������450�ǣ���ʱv= v0
v0
�ɼ��ι�ϵ����ȷ�������ڵ�һ���Ĺ���뾶Ϊr=2 L
L
����qvB=m �ɵ�
�ɵ� =
=
(3)�����ڵ�һ���ڶ������ڵĹ켣��ͼ��ʾ
���ӵ�����T=2�� -
-
���ӵ�һ���ڵ�һ�������˶���ʱ��t��
���Ӵ���x���ʱ��Ϊt=n +t��=
+t��= n��(0,1,2,����)
n��(0,1,2,����)
���㣺���⿼����������ڴų��е�Բ���˶����ڵ糡�е���ƽ���˶��Ĺ��ɣ����ڸ��ϳ�����ۺ���Ŀ��

 ��У����ϵ�д�
��У����ϵ�д�
 ����
����
 ��
��
 ������
������

 ��
��
 ������ֱֽ��������д�����������������ϵ����ٶ�
������ֱֽ��������д�����������������ϵ����ٶ� ��������������
�������������� ƽ�н���������糡�У��ų��߽�MN������
ƽ�н���������糡�У��ų��߽�MN������ ���������ܵ����������Ӽ��������������Բ��ƣ�
���������ܵ����������Ӽ��������������Բ��ƣ� ʱ������糡�Ĵ�������ǡ�ܴ�ƽ�н������Ե�������ô�����������糡ʱ���ٶȴ�С��
ʱ������糡�Ĵ�������ǡ�ܴ�ƽ�н������Ե�������ô�����������糡ʱ���ٶȴ�С�� ��
��
