题目内容
如图甲所示,两平行金属板的板长不超过0.2 m,板间的电压u随时间t变化的图线如图乙所示,在金属板右侧有一左边界为MN、右边无界的匀强磁场,磁感应强度 ,方向垂直纸面向里.现有带正电的粒子连续不断地以速度
,方向垂直纸面向里.现有带正电的粒子连续不断地以速度 ,沿两板间的中线
,沿两板间的中线 平行金属板射入电场中,磁场边界MN与中线
平行金属板射入电场中,磁场边界MN与中线 垂直.已知带电粒子的比荷
垂直.已知带电粒子的比荷 ,粒子所受的重力和粒子间的相互作用力均忽略不计.
,粒子所受的重力和粒子间的相互作用力均忽略不计.
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.试说明这种处理能够成立的理由.
(2)设 时刻射入电场的带电粒子恰能从平行金属板边缘射出,求该带电粒子射出电场时的速度大小.
时刻射入电场的带电粒子恰能从平行金属板边缘射出,求该带电粒子射出电场时的速度大小.
(3)对于所有经过电场射入磁场的带电粒子,设其射入磁场的入射点和从磁场射出的出射点间的距离为d,试判断d的大小是否随时间而变化?若不变,证明你的结论;若变,求出d的变化范围.

(1)带电粒子在金属板间运动时间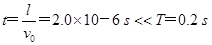 故t时间内金属板间的电场可以认为是恒定的.(2)
故t时间内金属板间的电场可以认为是恒定的.(2) 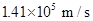
解析试题分析:(1)带电粒子在金属板间运动时间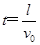 ,
,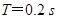 ①
①
得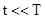 ,(或t时间内金属板间电压变化
,(或t时间内金属板间电压变化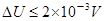 ,变化很小)②
,变化很小)②
故t时间内金属板间的电场可以认为是恒定的.
(2)  时刻偏转电压
时刻偏转电压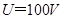
带电粒子沿两板间的中线射入电场恰从平行金属板边缘飞出电场,电场力做功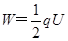 ③
③
由动能定理:  ④
④
代入数据可得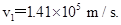 ⑤
⑤
(3)设某一任意时刻射出电场的粒子速率为v,速度方向与水平方向的夹角为α,则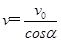 ⑥
⑥
粒子在磁场中有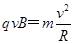 ⑦
⑦
可得粒子进入磁场后,在磁场中做圆周运动的半径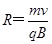
由几何关系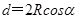 ⑧
⑧
可得: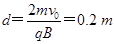 ,故d不随时间而变化.
,故d不随时间而变化.
考点:考查了带电粒子在组合场中的运动
点评:本题是组合场问题,综合应用动能定理、牛顿运动定律、运动学知识以及几何知识,中等难度

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案如图所示,边长为L的正方形单匝线圈abcd,电阻r,外电路的电阻为R,a、b的中点和cd的中点的连线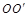 恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始,以角速度
恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始,以角速度 绕轴
绕轴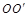 匀速转动,则以下判断正确的是
匀速转动,则以下判断正确的是 
A.图示位置线圈中的感应电动势最大为Em=BL2 |
B.闭合电路中感应电动势的瞬时值表达式为 |
C.线圈转动一周的过程中,电阻R上产生的热量为Q= |
D.线圈从图示位置转过180o的过程中,流过电阻R的电荷量为 |
如图所示,空间存在一有边界的条形匀强磁场区域,磁场方向与竖直平面(纸面)垂直,磁场边界的间距为L。一个质量为m、边长也为L的正方形导线框沿竖直方向运动,线框所在平面始终与磁场方向垂直,且线框上、下边始终与磁场的边界平行。t=0时刻导线框的上边恰好与磁场的下边界重合(图中位置I),导线框的速度为v0。经历一段时间后,当导线框的下边恰好与磁场的上边界重合时(图中位置Ⅱ),导线框的速度刚好为零。此后,导线框下落,经过一段时间回到初始位置I(不计空气阻力),则
| A.上升过程中合力做的功与下降过程中合力做的功相等 |
| B.上升过程中线框产生的热量比下降过程中线框产生的热量的多 |
| C.上升过程中,导线框的加速度逐渐减小 |
| D.上升过程克服重力做功的平均功率小于下降过程重力的平均功率 |
 1.0×10-4 C;带电粒子恰好从P点垂直AB边以速度v=2×105 m/s进入磁场,则
1.0×10-4 C;带电粒子恰好从P点垂直AB边以速度v=2×105 m/s进入磁场,则
 的取值在什么范围可以使带电微粒只能从BC边穿出?
的取值在什么范围可以使带电微粒只能从BC边穿出?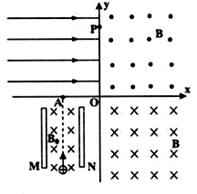

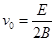 的初速度开始运动,并从P点离开磁场,此过程中运动到离过OP的直线最远位置时的加速度大小
的初速度开始运动,并从P点离开磁场,此过程中运动到离过OP的直线最远位置时的加速度大小 ,则此点离OP直线的距离是多少?
,则此点离OP直线的距离是多少? ,求该粒子离开磁场后到达y轴时的位置坐标.
,求该粒子离开磁场后到达y轴时的位置坐标.
 匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求
匀速移动,当与粒子相遇时粒子运动方向恰好与挡板平行,求
 ,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。
,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。