题目内容
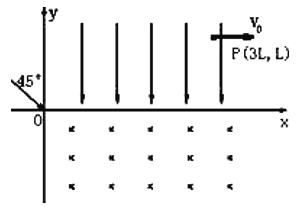
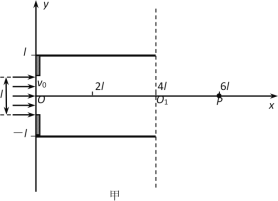
【题目】如图甲所示，两平行金属板间距为2l，长度为4l，O为两极板左侧的中点，OO1为两极板间的中心线，以O为坐标原点建立如图xOy直角坐标系。现将两极板间加如图乙所示的交变电压（t=0时上极板带正电）。从t=0时刻起，有一速度大小均为v0，区域宽度为l的平行电子束从左侧两极板正中央平行x轴不断入射，且所有电子均能从右侧两板间平行于x轴方向射出，有电子射出的区域宽度为2l。已知电子质量为m，电荷量为e，忽略电子之间的相互作用。试求：
（1）对于t=0时刻从O点射入的电子在离开两极板时的位置坐标；
（2）交变电压的周期T和电压U0的大小；
（3）为使所有电子会聚于P(6l，0)点，可在x≥4l区域加若干个垂直纸面的有界圆形匀强磁场，则确定磁感应强度B的范围。
【答案】(1)（4l，
）(2)
（k=1，2，3……）(3)
【解析】
（1）t=0时刻，从O点进入的电子离开两极板时的位置坐标为：（4l，）
（2）电子进入两金属板间做类平抛运动，由x轴方向知电子经过板间：
要使所有电子都能从右侧两板间平行x轴方向射出，则有：
t=kT
解得：
（k=1，2，3……）
在y轴方向有：
解得：
（k=1，2，3……）
（3）设电子进入圆形磁场的半径为R，磁感应强度为B，在磁场中做圆周运动，由洛伦兹力提供向心力：
磁感应强度的表达式为：
①当磁感应强度最大时，由图可知：2R=l
可得磁感应强度最大值：
②当磁感应强度最小时，由图可知：
可得磁感应强度最小值：
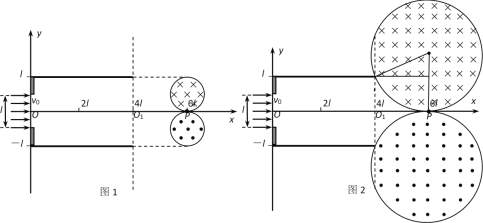
综上所述，为使所有电子会聚于P点，在x≥4l区域所加圆形匀强磁场的磁感应强度B的范围为：
练习册系列答案
相关题目
