题目内容
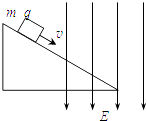
【题目】如图所示,一质量为m、带电量为q的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ角,重力加速度为g.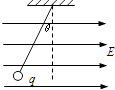
(1)判断小球带何种电荷.
(2)求电场强度E.
(3)若在某时刻将细线突然剪断,求经过t时间小球的速度v.
【答案】
(1)解:小球受到的电场力向左,与场强方向相反;
故小球带负电荷.
(2)解:对小球受力分析,受重力、电场力和拉力,如图

根据共点力平衡条件,有
qE=mgtanθ
故
![]()
![]()
即电场强度E为 ![]() .
.
(3)解:剪短细线后,小球受到重力和电场力,合力恒定,故做初速度为零的匀加速直线运动;
根据牛顿第二定律,有
F合=ma ①
由于三力平衡中,任意两个力的合力与第三力等值、反向、共线,故
F合= ![]() ②
②
根据速度时间公式,有
v=at ③
由①②③解得
![]()
即经过t时间小球的速度v为 ![]() .
.
【解析】(1)小球受到的电场力向左,与场强方向相反,故带负电荷;(2)对小球受力分析,然后根据共点力平衡条件列式求解出电场力,得到电场强度;(3)剪短细线后,小球受到重力和电场力,合力恒定,故做初速度为零的匀加速直线运动,根据牛顿第二定律求出加速度后,再运用速度时间公式求解.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目