题目内容
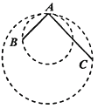
【题目】如图所示，在竖直平面内有半径为R和2R的两个圆，两圆的最高点相切，切点为A，B和C分别是小圆和大圆上的两个点，其中AB长为
，AC长为
．现沿AB和AC建立两条光滑轨道，自A处由静止释放小球，已知小球沿AB轨道运动到B点所用时间为t1，沿AC轨道运动到C点所用时间为t2，则t1与t2之比为（ ）
A．
B．1:2 C．
D．1:3
【答案】A
【解析】
试题分析：设AB与竖直方向的夹角为θ，则：AB=2Rcosθ，由牛顿第二定律得物体沿AB下滑的加速度为：a=gcosθ，解得在AB上运动的时间为：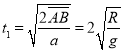
，同理设AB与竖直方向的夹角为α，则：AC=4Rcosα，由牛顿第二定律得物体沿AC下滑的加速度为：a=gcosα，可知物体在AC上运动的时间为：
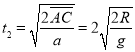．则
，故A正确。
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
