题目内容
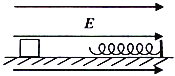
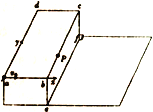
【题目】如图所示，长方体平台固定在水平地面上，平台ab边上L1=1.2m，bc边长L2=3.3m，be边长L3=0.8m。平台表面光滑，以平台表面倾角α为原点建立坐标系，ab边为x轴，ad边为y轴。一个质量m1=0.2kg的小球静止在平台表面的顶角a处，某时刻小球以v0=3m/s的初速度开始运动，v0的方向沿x轴正方向，同时小球受到一个沿y轴的水平外力F1，F1=5y(N)，当小球到达bc边上的P点时撤去外力F1，P点的坐标是(1.2m，0.8m)。在小球到达P点的同时，平台顶点c正下方f点处一个滑块以速度v在水平面上开始匀速直线运动，由于摩擦力的作用，要保证滑块匀速运动需要给滑块一个斜向上的外力F2，滑块的质量m2=0.2kg，滑块与水平面间的动摩擦因数μ=0.5。结果在小球落地时恰好与滑块相遇。小球、滑块均视为质点，取g=10m/s2.sin37°=0.6。求：
（1）小球到达P点时速度
的大小和方向；
（2）小球落在水平面的位置离f点的距离d；
（3）滑块运动的速度v和外力F2的最小值.
【答案】（1）5m/s；37°（2）1.5m（3）3.75 m/s；0.9N
【解析】（1）小球在平台上作曲线运动，可分解为沿x轴方向的匀速直线运动和沿y轴方向的变加速运动。设小球在P点速度与y轴夹角为α。
变力F1的功
J
J
从a点到P点，据动能定理有
，解得
由
，得sin α=06，即α=37°
（2）小球在P处开始作平抛运动，根据平抛运动的规律，有
，解得
s
水平位移
，解得s=2m
设小球落在水平面的位置离f点的距离为d，根据余弦定理，有
，解得d=15 m
（3）小球落点设为R点，滑块要与小球相遇，滑块必须沿f R连线运动，由匀速直线运动的规律得
，解得v=375 m/s
设外力F2的方向与滑块运动方向的夹角为β，根据平衡条件有
， 
联立解得
据数学知识可得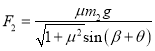
，其最小值
即
N
