Question

【题目】如图所示，传送带与地面倾角θ＝37°，从A到B长度为L＝10.25m，传送带以v0＝10m/s的速率逆时针转动。在传送带上端A无初速度地放一个质量为m＝0.5kg的黑色煤块，它与传送带之间的动摩擦因数为μ＝0.5．煤块在传送带上经过会留下黑色痕迹。已知sin37°＝0.6，g＝10m/s2，求：煤块从A到B的时间；

Answer 1

【答案】1.5s

【解析】

煤块刚放上时，受到向下的摩擦力，如图如图所示，其加速度为a1，

根据牛顿第二定律有：mgsinθ+μmgcosθ＝ma1

代入数据解得：

a1=10m/s2

匀加速运动到与传送带速度相等的时间为t1，则有：

即下滑5m与传送带速度相等。

达到v0后，受到向上的摩擦力，由于μ＜tan37°，煤块仍将加速加速下滑，如图所示：

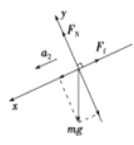
根据牛顿第二定律有：mgsinθμmgcosθ＝ma2

代入数据解得：

a2=2m/s2

继续做匀加速运动的位移为：

根据位移公式得：

代入数据解得：

t2=0.5s

煤块从A到B的时间为：

t=t1+t2=1.5s