��Ŀ����
8��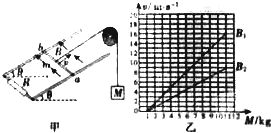 ��ͼ����ʾ������������һϸ�ߣ��ߵ�һ��ϵһ����ΪM�������һ��ϵһ����Ϊm�Ľ�������������ab�����������ΪL���㹻���Ĺ⻬ƽ�н��������ϣ�������ˮƽ����ļн�Ϊ�ȣ����������֮����������ֵΪR�ĵ��衢����ͽ������ĵ��費�ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų��뵼��ƽ�洹ֱ���ϣ���ʼʱ���������ڵ����¶ˣ��������ɾ�ֹ�ͷţ����������������»����˶������н�����ʼ���������촹ֱ�ҽӴ����ã���֪�������ٶ�Ϊg����
��ͼ����ʾ������������һϸ�ߣ��ߵ�һ��ϵһ����ΪM�������һ��ϵһ����Ϊm�Ľ�������������ab�����������ΪL���㹻���Ĺ⻬ƽ�н��������ϣ�������ˮƽ����ļн�Ϊ�ȣ����������֮����������ֵΪR�ĵ��衢����ͽ������ĵ��費�ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų��뵼��ƽ�洹ֱ���ϣ���ʼʱ���������ڵ����¶ˣ��������ɾ�ֹ�ͷţ����������������»����˶������н�����ʼ���������촹ֱ�ҽӴ����ã���֪�������ٶ�Ϊg������1�������������½�ʱ���ٶȴ�С��
��2����M�����˶�ʱ��ͻȻ����ϸ�ߣ������������ص��������˶�����������һ�ξ���s��ﵽ��ߵ㣬��˹����е���R�ϲ����Ľ����ȣ�
��3����һ���ĴŸ�Ӧǿ��B������ȡ��ͬ������M�������Ӧ�������������½��˶�ʱ��vֵ���õ�ʵ��ͼ����ͼ����ʾ��ͼ�л����˴Ÿ�Ӧǿ�ȷֱ�ΪB1��B2ʱ������ʵ��ͼ�ߣ��Ը���ʵ���������ֵ$\frac{{B}_{1}}{{B}_{2}}$��
���� ��1�����������½�ʱ����������������������Ϊ�㣮���������˵������������F=BIL��I=$\frac{E}{R}$��E=BLv����Ƶ����������ı���ʽ��������ƽ������������������½����ٶ�v��
��2����M�Ӿ�ֹ�����ٵĹ������½��߶�h�Ĺ����У�M���������ܼ�Сת��Ϊm���������ܡ�ϵͳ�Ķ��ܺ����ܣ����������غ㶨�����R�ϲ����Ľ����ȣ�
��3�����ݵ�1��v�ı���ʽ������v-Mͼ���б�ʣ����ͼ�����б�ʣ����ɵõ�B1��B2�ı�ֵ��
��� �⣺��1�������������½�ʱ���ٶȴ�СΪv��
�����˴ﵽ�����˶�ʱ������������F�������˵�����mg�����µİ�����FA��
��F=FA+mgsin�ȡ���
����F=Mg����
�ֶԽ������У�������FA=BIL����Ӧ����I=$\frac{E}{R}$����Ӧ�綯�� E=BLv
��ã�FA=$\frac{{B}^{2}{L}^{2}v}{R}$����
�����ɢ٢ڢ۵ã�v=$\frac{��M-msin�ȣ�gR}{{B}^{2}{L}^{2}}$����
��2������ϸ�ߺԽ������ͻ�·ϵͳ�������Ľ�����ΪQ���������غ�ã�
$\frac{1}{2}m{v}^{2}$=mgssin��+Q
��� Q=$\frac{m��M-msin�ȣ�^{2}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$-mgssin��
��3�����ݵ�1����õĽ����֪���ɢ�ʽ�ɵ�v-M��б��Ϊ k=$\frac{gR}{{B}^{2}{L}^{2}}$
��ͼ�ҿɵ� k1=$\frac{8}{5}$m/s•kg��k2=$\frac{9}{10}$m/s•kg
�ɵ� $\frac{{B}_{1}}{{B}_{2}}$=$\sqrt{\frac{{k}_{2}}{{k}_{1}}}$
�������ݽ�� $\frac{{B}_{1}}{{B}_{2}}$=$\frac{3}{4}$
��
��1�����������½�ʱ���ٶȴ�СΪ$\frac{��M-msin�ȣ�gR}{{B}^{2}{L}^{2}}$��
��2����M�����˶�ʱ��ͻȻ����ϸ�ߣ������������ص��������˶�����������һ�ξ��룬��ﵽ��ߵ㣬�˹����е���R�ϲ����Ľ�����Ϊ$\frac{m��M-msin�ȣ�^{2}{g}^{2}{R}^{2}}{2{B}^{4}{L}^{4}}$-mgssin�ȣ�
��3����ֵ$\frac{{B}_{1}}{{B}_{2}}$Ϊ$\frac{3}{4}$��
���� ����������F=BIL��I=$\frac{E}{R}$��E=BLv�Ƶ��������ı���ʽ�����Ĺؼ����裬��������ѧ֪ʶ����ͼ���б�ʣ��õ�B1��B2�ı�ֵ��

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�| A�� | �������������з������� | |
| B�� | �������ͷ�������Ҳ����������ͬһ������ | |
| C�� | ��С��ȡ������෴������ͬһֱ���ϵ�������һ�����������ͷ������� | |
| D�� | �������ͷ�������һ����С��ȡ������෴������ͬһֱ���� |
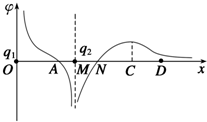 ��������ֱ�Ϊq1��q2�ĵ��ɷ���x����O��M���㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ������A��N����ĵ���Ϊ�㣬ND����C�������ߣ�������˵������ȷ���ǣ�������
��������ֱ�Ϊq1��q2�ĵ��ɷ���x����O��M���㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ������A��N����ĵ���Ϊ�㣬ND����C�������ߣ�������˵������ȷ���ǣ�������| A�� | q1�����磬q2������ | |
| B�� | |q1|=|q2| | |
| C�� | A��ĵ糡ǿ�ȴ�СΪ�� | |
| D�� | ��һ�����ɴ�N���Ƶ�D�㣬�糡������������������ |
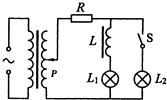 ��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ���н�����Դ������Ȧ��ͨ������߽��е���Ll��L2�ͺ�����о����ȦL������ߵ�Ч����ΪR����ʼʱ������S�Ͽ�����ƬP����ͼʾλ�ã�����L1�ܷ��⣮Ҫʹ����L1���������Բ�ȡ�İ취�ǣ�������| A�� | ���ϻ���P | B�� | �պϿ���S | ||
| C�� | �����Ȧ�е���о | D�� | ��������Դ��Ƶ�� |
| A�� | $\sqrt{\frac{n}{k}}$T | B�� | $\sqrt{\frac{{n}^{2}}{k}}$T | C�� | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D�� | $\sqrt{\frac{{n}^{3}}{k}}$T |
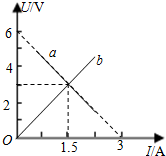 ��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A��
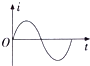
��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A��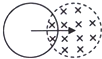 ��ͼ��ʾ���뾶ΪR��Բ�ε������ġ����ٴ����뾶ҲΪR��Բ����ǿ�ų����涨��ʱ�뷽��ĸ�Ӧ����Ϊ���������и�Ӧ����i��ʱ��t�ı仯��ϵͼ�������ʵ�ʵ��ǣ�������
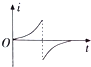
��ͼ��ʾ���뾶ΪR��Բ�ε������ġ����ٴ����뾶ҲΪR��Բ����ǿ�ų����涨��ʱ�뷽��ĸ�Ӧ����Ϊ���������и�Ӧ����i��ʱ��t�ı仯��ϵͼ�������ʵ�ʵ��ǣ�������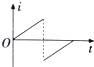
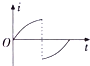
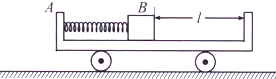 ��ͼ��ʾ��һ������M=3kg��С��A��ֹ��ˮƽ���ϣ�С������һ����m=1kg��С���B����һ���ʵ���ѹ������������ʱ���ɵĵ�������ΪEp=6J��С�����С���ұھ���Ϊl=0.4m�����������С������뵯�ɺ���С���ұڷ�����ײ����ײ������е����ʧ������һ��Ħ������
��ͼ��ʾ��һ������M=3kg��С��A��ֹ��ˮƽ���ϣ�С������һ����m=1kg��С���B����һ���ʵ���ѹ������������ʱ���ɵĵ�������ΪEp=6J��С�����С���ұھ���Ϊl=0.4m�����������С������뵯�ɺ���С���ұڷ�����ײ����ײ������е����ʧ������һ��Ħ������