题目内容
18.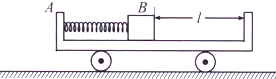 如图所示,一辆质量M=3kg的小车A静止在水平面上,小车上有一质量m=1kg的小物块B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小物块与小车右壁距离为l=0.4m,解除锁定,小物块脱离弹簧后与小车右壁发生碰撞,碰撞过程无机械能损失,不计一切摩擦.求:
如图所示,一辆质量M=3kg的小车A静止在水平面上,小车上有一质量m=1kg的小物块B,将一轻质弹簧压缩并锁定,此时弹簧的弹性势能为Ep=6J,小物块与小车右壁距离为l=0.4m,解除锁定,小物块脱离弹簧后与小车右壁发生碰撞,碰撞过程无机械能损失,不计一切摩擦.求:①从解除锁定到小物块与小车右壁发生第一次碰撞,小车移动的距离;
②小物块与小车右壁发生碰撞后,小物块和小车各自的速度大小和方向.
分析 根据动量守恒定律和能量守恒定律求出小球脱离弹射装置时小球和小车各自的速度大小.
解答 解:①设小车移动的距离为x1,小物块移动的距离为x2,从解除锁定到小物块与小车右壁碰撞过程中,水平面光滑,
由小车、弹簧和小物块组成的系统动量守恒,所以有:
m$\frac{{x}_{2}}{t}$-M$\frac{{x}_{1}}{t}$=0
由运动关系可得:x1+x2=l,
解得:x1=$\frac{m}{m+M}$l=0.1m
②水平面光滑,由小车、弹簧和小物块组成的系统在从弹簧解锁到小物块脱离弹簧的过程中,满足动量守恒和能量守恒,
选向右为正方向,即:mv2+Mv1=0,
Ep=$\frac{1}{2}$m${v}_{2}^{2}$+$\frac{1}{2}$M${v}_{1}^{2}$
解得v1=1m/s,v2=-3m/s.
所以碰后小车速度方向向右为1m/s,小物块速度方向向左为3m/s,
答:①从解除锁定到小物块与小车右壁发生第一次碰撞,小车移动的距离是0.1m;
②碰后小车速度方向向右为1m/s,小物块速度方向向左为3m/s.
点评 本题是动量守恒和能量守恒的综合应用.解除弹簧的锁定后,系统所受合力为零,遵守动量守恒和能量守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )| A. | 如果y表示加速度,则面积等于质点t0在时刻的速度 | |
| B. | 如果y表示流过用电器的电流,则面积等于在相应时间内该用电器消耗的电能 | |
| C. | 如果y表示力做功的功率,则面积等于该力在相应时间内所做的功 | |
| D. | 如果y表示变化磁场在金属线圈中产生的电动势,则面积等于该磁场在相应时间内磁感应强度的变化量 |
10.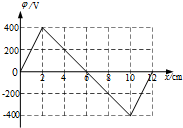 在某一静电场中建立x轴,其电势随坐标x变化的图线如图所示.若将一带负电的粒子(重力不计)从坐标原点O处由静止释放,电场中P、Q两点位于x轴上,其横坐标分别为1cm、4cm.则下列说法正确的是( )
在某一静电场中建立x轴,其电势随坐标x变化的图线如图所示.若将一带负电的粒子(重力不计)从坐标原点O处由静止释放,电场中P、Q两点位于x轴上,其横坐标分别为1cm、4cm.则下列说法正确的是( )
 在某一静电场中建立x轴,其电势随坐标x变化的图线如图所示.若将一带负电的粒子(重力不计)从坐标原点O处由静止释放,电场中P、Q两点位于x轴上,其横坐标分别为1cm、4cm.则下列说法正确的是( )
在某一静电场中建立x轴,其电势随坐标x变化的图线如图所示.若将一带负电的粒子(重力不计)从坐标原点O处由静止释放,电场中P、Q两点位于x轴上,其横坐标分别为1cm、4cm.则下列说法正确的是( )| A. | 粒子恰能运动到离原点12cm处 | |
| B. | 粒子经过P点与Q点时,动能相等 | |
| C. | 粒子经过P、Q两点时,加速度大小之比2:1 | |
| D. | 粒子经过P、Q两点时,电场力功率之比1:1 |
7.下列关于近代物理知识的描述中,正确的是( )
| A. | 若用蓝色光照射某金属表面时有电子逸出,则改用紫光照射也一定会有电子逸出 | |
| B. | 处于n=3能级状态的某个氢原子自发跃迁时,能发出3种频率的光子 | |
| C. | 衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| D. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+X核反应中,X是质子,这个反应过程叫原子核的人工转变 | |
| E. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 |
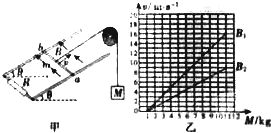 如图甲所示,定滑轮上绕一细线,线的一端系一质量为M的重物,另一端系一质量为m的金属棒,金属棒ab放在两根间距为L的足够长的光滑平行金属导轨上,导轨与水平方向的夹角为θ,在两导轨底端之间连接有阻值为R的电阻、导轨和金属棒的电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直向上.开始时金属杆置于导轨下端,将重物由静止释放,重物最终能匀速下滑.运动过程中金属杆始终与两导轨垂直且接触良好,已知重力加速度为g;求:
如图甲所示,定滑轮上绕一细线,线的一端系一质量为M的重物,另一端系一质量为m的金属棒,金属棒ab放在两根间距为L的足够长的光滑平行金属导轨上,导轨与水平方向的夹角为θ,在两导轨底端之间连接有阻值为R的电阻、导轨和金属棒的电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直向上.开始时金属杆置于导轨下端,将重物由静止释放,重物最终能匀速下滑.运动过程中金属杆始终与两导轨垂直且接触良好,已知重力加速度为g;求: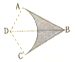 如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求:
如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求: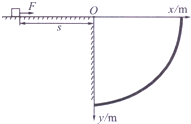 如图所示,一质量m=1.0kg的小物块静止在粗糙水平台阶上,离台阶边缘O点的距离s=5m,它与水平台阶表面的动摩擦因数μ=0.25.在台阶右侧固定一个以O为圆心的 $\frac{1}{4}$圆弧挡板,圆弧半径R=5$\sqrt{2}$m,以O点为原点建立平面直角坐标系xOy.现用F=5N的水平恒力拉动小物块(已知重力加速度g=10m/s2).
如图所示,一质量m=1.0kg的小物块静止在粗糙水平台阶上,离台阶边缘O点的距离s=5m,它与水平台阶表面的动摩擦因数μ=0.25.在台阶右侧固定一个以O为圆心的 $\frac{1}{4}$圆弧挡板,圆弧半径R=5$\sqrt{2}$m,以O点为原点建立平面直角坐标系xOy.现用F=5N的水平恒力拉动小物块(已知重力加速度g=10m/s2).
 如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )
如图所示是示波器原理图,电子被电压为U1的加速电场加速后射入电压为U2的偏转电场,离开偏转电场后电子打在荧光屏上的P点,P点与O点的距离叫做偏转距离,偏转电场极板长为L,板间距离为d,为了增大偏转距离,下列措施可行的是( )