题目内容
17.双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量?距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为( )| A. | $\sqrt{\frac{n}{k}}$T | B. | $\sqrt{\frac{{n}^{2}}{k}}$T | C. | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D. | $\sqrt{\frac{{n}^{3}}{k}}$T |
分析 双星靠相互间的万有引力提供向心力,具有相同的角速度,根据牛顿第二定律分别对两星进行列式,来求解.
解答 解:设m1的轨道半径为R1,m2的轨道半径为R2.两星之间的距离为L.
由于它们之间的距离恒定,因此双星在空间的绕向一定相同,同时角速度和周期也都相同.由向心力公式可得:
对m1:G$\frac{{{m}_{1}m}_{2}}{{L}^{2}}$=m1$\frac{{4π}^{2}}{{T}^{2}}$R1…①
对m2:G$\frac{{{m}_{1}m}_{2}}{{L}^{2}}$=m2$\frac{{4π}^{2}}{{T}^{2}}$R2…②
又因为R1+R2=L,m1+m2=M
由①②式可得:T=2π$\sqrt{\frac{{L}^{3}}{GM}}$
所以当两星总质量变为KM,两星之间的距离变为原来的n倍,所以此时圆周运动的周期为$\sqrt{\frac{{n}^{3}}{k}}$,
故选:D.
点评 解决本题的关键知道双星靠相互间的万有引力提供向心力,具有相同的角速度,能运用万有引力提供向心力进行解题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
7.下列物理量的单位中,属于国际单位制中的基本单位的是( )
| A. | 牛顿 | B. | 秒 | C. | 焦耳 | D. | 瓦 |
2.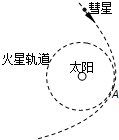 据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
 据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )
据报道,一颗来自太阳系外的彗星于2014年10月20日擦火星而过.如图所示,设火星绕太阳在圆轨道上运动,运动半径为r,周期为T.该彗星在穿过太阳系时由于受到太阳的引力,轨道发生弯曲,彗星与火星在圆轨道的A点“擦肩而过”.已知万有引力恒量G,则( )| A. | 可计算出彗星的质量 | |
| B. | 可计算出彗星经过A点时受到的引力 | |
| C. | 可计算出彗星经过A点的速度大小 | |
| D. | 可确定彗星在A点的速度大于火星绕太阳的速度 |
6. 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
 微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )
微元累积法是常用的物理研究方法,如图所示为某物理量随时间变化的函数图象,关于此图线与两坐标轴围成面积的物理意义,下列说法正确的是( )| A. | 如果y表示加速度,则面积等于质点t0在时刻的速度 | |
| B. | 如果y表示流过用电器的电流,则面积等于在相应时间内该用电器消耗的电能 | |
| C. | 如果y表示力做功的功率,则面积等于该力在相应时间内所做的功 | |
| D. | 如果y表示变化磁场在金属线圈中产生的电动势,则面积等于该磁场在相应时间内磁感应强度的变化量 |
7.下列关于近代物理知识的描述中,正确的是( )
| A. | 若用蓝色光照射某金属表面时有电子逸出,则改用紫光照射也一定会有电子逸出 | |
| B. | 处于n=3能级状态的某个氢原子自发跃迁时,能发出3种频率的光子 | |
| C. | 衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| D. | 在${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+X核反应中,X是质子,这个反应过程叫原子核的人工转变 | |
| E. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 |
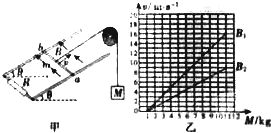 如图甲所示,定滑轮上绕一细线,线的一端系一质量为M的重物,另一端系一质量为m的金属棒,金属棒ab放在两根间距为L的足够长的光滑平行金属导轨上,导轨与水平方向的夹角为θ,在两导轨底端之间连接有阻值为R的电阻、导轨和金属棒的电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直向上.开始时金属杆置于导轨下端,将重物由静止释放,重物最终能匀速下滑.运动过程中金属杆始终与两导轨垂直且接触良好,已知重力加速度为g;求:
如图甲所示,定滑轮上绕一细线,线的一端系一质量为M的重物,另一端系一质量为m的金属棒,金属棒ab放在两根间距为L的足够长的光滑平行金属导轨上,导轨与水平方向的夹角为θ,在两导轨底端之间连接有阻值为R的电阻、导轨和金属棒的电阻不计,磁感应强度为B的匀强磁场与导轨平面垂直向上.开始时金属杆置于导轨下端,将重物由静止释放,重物最终能匀速下滑.运动过程中金属杆始终与两导轨垂直且接触良好,已知重力加速度为g;求: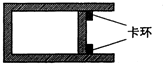 如图所示,一内壁光滑的气缸固定于水平地面上,在距气缸底部L=54cm处有一固定于气缸上的卡环,活塞与气缸底部之间封闭着一定质量的理想气体,活塞在图示位置时封闭气体的温度t1=267℃,压强p1=1.5atm.设大气压强ρ0恒为1atm,气缸导热性能良好,不计活塞的厚度.由于气缸缓慢放热,活塞最终会左移到某一位置而平衡.求
如图所示,一内壁光滑的气缸固定于水平地面上,在距气缸底部L=54cm处有一固定于气缸上的卡环,活塞与气缸底部之间封闭着一定质量的理想气体,活塞在图示位置时封闭气体的温度t1=267℃,压强p1=1.5atm.设大气压强ρ0恒为1atm,气缸导热性能良好,不计活塞的厚度.由于气缸缓慢放热,活塞最终会左移到某一位置而平衡.求
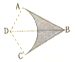 如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求:
如图所示,ABC为一透明材料做出的柱形光学元件的横截面,D为AC圆弧的圆心,∠ADC=120°,∠ABC=60°,AB=BC,B、D间的距离为d.D处点光源发出的光中有一束光线经AB、BC界面两次全反射后,光束恰好通过D点.求: