题目内容
 如图所示,在磁感强度B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环.圆环所在的平面与磁感线垂直.OA是一个金属棒,它沿着顺时针方向以20rad/s的角速度绕圆心O匀速转动.A端始终与圆环相接触OA棒的电阻R=0.1Ω,图中定值电阻R1=100Ω,R2=4.9Ω,电容器的电容C=100pF.圆环和连接导线的电阻忽略不计,求:
如图所示,在磁感强度B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环.圆环所在的平面与磁感线垂直.OA是一个金属棒,它沿着顺时针方向以20rad/s的角速度绕圆心O匀速转动.A端始终与圆环相接触OA棒的电阻R=0.1Ω,图中定值电阻R1=100Ω,R2=4.9Ω,电容器的电容C=100pF.圆环和连接导线的电阻忽略不计,求:(1)电容器的带电量.哪个极板带正电.
(2)电路中消耗的电功率是多少?
分析:本题(1)的关键是明确导体棒以一端为轴做旋转切割磁感线运动时感应电动势的求法,为E=
,然后根据电路图求出总电流和电容器两端的电压即可,再根据右手定则判定电容器两板电势的高低;题(2)的关键是明确电路中消耗的电功率的含义是
=EI.
| ||
| 2 |
| P | 总 |
解答:解:(l)导体棒OA产生感应电动势为:E=BL
=Br
=
代入数据解得:E=5V,
根据闭合电路欧姆定律可得总电流为:I=
=
A=1A
由欧姆定律可知电容器两端电压为:
=
=1×4.9V=4.9V
所以电容器带电量为:Q=C
=100
×4.9C=4.9
C
根据右手定则可知,A点电势高于O点电势,电容器上板为正极.
(2)电路中消耗的电功率为:
=EI=5×1W=5W
答:(1)电容器的带电量为4.9
C,电容器上板为正极.
(2)电路中消耗的电功率是5W.
. |
| v |
| rw |
| 2 |
| ||
| 2 |
代入数据解得:E=5V,
根据闭合电路欧姆定律可得总电流为:I=
| E | ||
R
|
| 5 |
| 0.1+4.9 |
由欧姆定律可知电容器两端电压为:
| U | c |
| IR | 2 |
所以电容器带电量为:Q=C
| U | c |
| ×10 | -12 |
| ×10 | -10 |
根据右手定则可知,A点电势高于O点电势,电容器上板为正极.
(2)电路中消耗的电功率为:
| P | 消 |
答:(1)电容器的带电量为4.9
| ×10 | -10 |
(2)电路中消耗的电功率是5W.
点评:熟记导体棒以一端为轴做切割磁感线运动时产生的感应电动势表达式为E=
.
B
| ||
| 2 |

练习册系列答案
相关题目
 如图所示,在磁感强度为B的匀强磁场中,有一个边长为L的正六边形线圈,线圈平面垂直于磁场方向,线圈通有顺时针方向的电流,电流强度大小为I,则线圈所受安培力的大小为
如图所示,在磁感强度为B的匀强磁场中,有一个边长为L的正六边形线圈,线圈平面垂直于磁场方向,线圈通有顺时针方向的电流,电流强度大小为I,则线圈所受安培力的大小为 如图所示,在磁感强度为B、方向垂直纸面向里的匀强磁场中,有一竖直放置的光滑导电轨道,轨道间接有电阻R.套在轨道上的金属杆ab,长为L、质量为M、电阻为r.现用竖直向上的拉力,使ab杆沿轨道以速度v匀速上滑(轨道电阻不计).
如图所示,在磁感强度为B、方向垂直纸面向里的匀强磁场中,有一竖直放置的光滑导电轨道,轨道间接有电阻R.套在轨道上的金属杆ab,长为L、质量为M、电阻为r.现用竖直向上的拉力,使ab杆沿轨道以速度v匀速上滑(轨道电阻不计).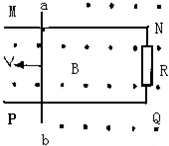 如图所示,在磁感强度B=0.5T,方向竖直向上的某匀强磁场中,垂直于磁场方向的同一水平面内放置两根不计电阻的平行金属导轨MN和PQ,两导轨间距离为d=0.1m,在两导轨端点N、Q间接一电阻R=0.3Ω,再在导轨上垂直放置一根长L=0.2m,总电阻r=0.2Ω的金属棒ab,当棒ab以v=4m/s的速度向左匀速运动时,试求:
如图所示,在磁感强度B=0.5T,方向竖直向上的某匀强磁场中,垂直于磁场方向的同一水平面内放置两根不计电阻的平行金属导轨MN和PQ,两导轨间距离为d=0.1m,在两导轨端点N、Q间接一电阻R=0.3Ω,再在导轨上垂直放置一根长L=0.2m,总电阻r=0.2Ω的金属棒ab,当棒ab以v=4m/s的速度向左匀速运动时,试求: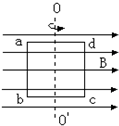 如图所示,在磁感强度B=10T的匀强磁场中有一匝数为n=100的矩形线圈abcd,其电阻R=10Ω,初始放置时线圈平面与磁感线平行,已知线圈ab=15cm,ad=10cm,线圈绕对称轴OO’转动,且角速度为314rad/s.求:
如图所示,在磁感强度B=10T的匀强磁场中有一匝数为n=100的矩形线圈abcd,其电阻R=10Ω,初始放置时线圈平面与磁感线平行,已知线圈ab=15cm,ad=10cm,线圈绕对称轴OO’转动,且角速度为314rad/s.求: