题目内容
如图所示，在磁感强度为B、方向垂直纸面向里的匀强磁场中，有一竖直放置的光滑导电轨道，轨道间接有电阻R．套在轨道上的金属杆ab，长为L、质量为M、电阻为r．现用竖直向上的拉力，使ab杆沿轨道以速度v匀速上滑（轨道电阻不计）．（1）所用拉力F的大小．
（2）ab杆两端电压Uab的大小
（3）拉力F的功率．
（4）电阻R消耗的电功率．
分析：1、根据金属杆切割磁感线产生的感应电动势可计算出感应电流，从而求得安培力．由于金属杆做匀速运动，故受力平衡，即F=Mg+F安．
2、金属杆ab相当于电源，ab两端的电压相当于电源的路端电压，所以Uab=IR．
3、根据力做功的功率的公式P=Fv，直接计算即可．
4、电阻R消耗的电功率等于PR=
，根据前面计算的电压值代入计算．
2、金属杆ab相当于电源，ab两端的电压相当于电源的路端电压，所以Uab=IR．
3、根据力做功的功率的公式P=Fv，直接计算即可．
4、电阻R消耗的电功率等于PR=
| Uab2 |
| R |
解答：解：（1）金属杆产生的感应电动势为：E=BLv
根据欧姆定律，通过金属杆的电流为：I=
=
根据左手定则，金属杆受到安培力竖直向下，大小为：F=BId=B
d．
由于金属杆做匀速直线运动，根据平衡条件有：F=Mg+F安．
解得：F=Mg+
（2）金属杆ab相当于电源，ab两端的电压相当于电源的路端电压，即R两端的电压，有：
Uab=IR=
?R=
（3）拉力的功率为：P=Fv=(Mg+
)v=Mgv+
（4）根据电功率的计算公式得：P=PR=
=
=
答：（1）所用拉力F的大小为Mg+
．
（2）ab杆两端电压Uab的大小为
．
（3）拉力F的功率为Mgv+
．
（4）电阻R消耗的电功率为
．
根据欧姆定律，通过金属杆的电流为：I=
| E |
| R+r |
| BLv |
| R+r |
根据左手定则，金属杆受到安培力竖直向下，大小为：F=BId=B
| BLv |
| R+r |
由于金属杆做匀速直线运动，根据平衡条件有：F=Mg+F安．
解得：F=Mg+
| B2L2v |
| R+r |
（2）金属杆ab相当于电源，ab两端的电压相当于电源的路端电压，即R两端的电压，有：
Uab=IR=
| BLv |
| R+r |
| BLvR |
| R+r |
（3）拉力的功率为：P=Fv=(Mg+
| B2L2v |
| R+r |
| B2L2v2 |
| R+r |
（4）根据电功率的计算公式得：P=PR=
| Uab2 |
| R |
(
| ||
| R |
| B2L2v2R |
| (R+r)2 |
答：（1）所用拉力F的大小为Mg+
| B2L2v |
| R+r |
（2）ab杆两端电压Uab的大小为
| BLvR |
| R+r |
（3）拉力F的功率为Mgv+
| B2L2v2 |
| R+r |
（4）电阻R消耗的电功率为
| B2L2v2R |
| (R+r)2 |
点评：本题是电磁感应中的动力学问题和电路问题的综合题，关键要分析清楚金属杆的受力情况，有一定的难度，属于中档题．
练习册系列答案
相关题目
如图所示，在磁感强度B=2T的匀强磁场中，有一个半径r=0.5m的金属圆环．圆环所在的平面与磁感线垂直．OA是一个金属棒，它沿着顺时针方向以20rad/s的角速度绕圆心O匀速转动．A端始终与圆环相接触OA棒的电阻R=0.1Ω，图中定值电阻R1=100Ω，R2=4.9Ω，电容器的电容C=100pF．圆环和连接导线的电阻忽略不计，求：
如图所示，在磁感强度为B的匀强磁场中，有一个边长为L的正六边形线圈，线圈平面垂直于磁场方向，线圈通有顺时针方向的电流，电流强度大小为I，则线圈所受安培力的大小为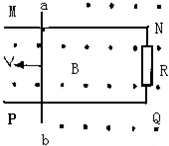
如图所示，在磁感强度B=0.5T，方向竖直向上的某匀强磁场中，垂直于磁场方向的同一水平面内放置两根不计电阻的平行金属导轨MN和PQ，两导轨间距离为d=0.1m，在两导轨端点N、Q间接一电阻R=0.3Ω，再在导轨上垂直放置一根长L=0.2m，总电阻r=0.2Ω的金属棒ab，当棒ab以v=4m/s的速度向左匀速运动时，试求：
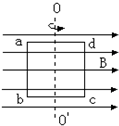如图所示，在磁感强度B=10T的匀强磁场中有一匝数为n=100的矩形线圈abcd，其电阻R=10Ω，初始放置时线圈平面与磁感线平行，已知线圈ab=15cm，ad=10cm，线圈绕对称轴OO’转动，且角速度为314rad/s．求：