题目内容

一列简谐横波沿直线AB传播,如图所示方向由A指向B,传播速度为340m/s,波频率为680Hz,a、b是AB上的两质点,相距L=25cm,当波传到质点a时,质点a从平衡位置以6m/s速度向上运动,振幅为0.1cm,求:
(1)质点a第一次运动到上方极端位置过程中的平均速度;
(2)若质点a从开始运动到某时刻的路程为1.02cm,则这时刻质点b的位置在何处?这段时间内通过的路程为多少?
分析:(1)质点a第一次运动到上方极端位置过程中通过的位移等于振幅A,时间为
周期.由平均速度公式
=
求解.
(2)由波速公式v=λf求出波长,根据ab间距离L与波长的关系,分析它们状态的关系.根据质点做简谐运动时,一个周期内通过的路程是4A,分析质点a从开始运动到某时刻的路程为1.02cm时所用的时间,再根据时间与周期的关系,判断这时刻质点b的位置.并确定路程.
解答:解:(1)该波的周期为T=
=
s
质点a第一次运动到上方极端位置过程中通过的位移x=A=0.1cm=0.001m,时间为t=
T=
s,则平均速度为
=
=
m/s=0.17m/s.
(2)由v=λf得,λ=
=
m=0.5m
因ab两质点的相距L=25cm=0.5λ,所以ab两质点的振动情况总是相反.
质点a从开始运动到某时刻的路程为S=1.02cm=10.2A,到达平衡位置下方0.2A=0.02cm处,b点到达平衡位置上方0.02cm处.
这段时间内b点通过的路程是10.2A-2A=8.2×0.1cm=0.82cm
答:
(1)质点a第一次运动到上方极端位置过程中的平均速度是0.17m/s;
(2)若质点a从开始运动到某时刻的路程为1.02cm,则这时刻质点b的位置在平衡位置上方0.02cm处,这段时间内通过的路程为0.82cm.
点评:解决本题关键有两点:一是分析a质点的运动情况,确定其位移;二是找出两个质点状态关系,求解b的位置和路程.
练习册系列答案
相关题目
 一列简谐横波沿直线AB传播,如图所示方向由A指向B,传播速度为340m/s,波频率为680Hz,a、b是AB上的两质点,相距L=25cm,当波传到质点a时,质点a从平衡位置以6m/s速度向上运动,振幅为0.1cm,求:
一列简谐横波沿直线AB传播,如图所示方向由A指向B,传播速度为340m/s,波频率为680Hz,a、b是AB上的两质点,相距L=25cm,当波传到质点a时,质点a从平衡位置以6m/s速度向上运动,振幅为0.1cm,求:
 应用题作业本系列答案
应用题作业本系列答案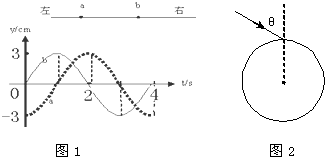 (1)一列简谐横波沿直线A、b向右传播,A、、b两点之间沿波的传播方向的距离为2m,A、、b两点的振动情况如图1所示,下列说法中正确的是
(1)一列简谐横波沿直线A、b向右传播,A、、b两点之间沿波的传播方向的距离为2m,A、、b两点的振动情况如图1所示,下列说法中正确的是


 .
.



 .
.
