题目内容
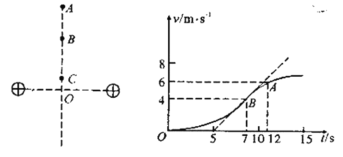
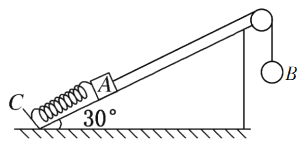
【题目】如图所示,在倾角为30°的光滑斜面上,劲度系数为k的轻质弹簧一端连接固定挡板C,另一端连接质量为m的物体A,一轻质细绳通过定滑轮,一端系在物体A上,另一端与质量也为m的物休B相连,细绳与斜面平行,斜面足够长,用手托住物休B使细绳刚好没有拉力,然后由静止释放物体B(运动过程中物体B未落地),则:
A. 物体B运动到最低点时,细绳上的拉力为mg
B. 弹簧恢复原长时,细绳上的拉力为![]() mg
mg
C. 物体A沿斜面向上运动的最大速度为![]()
D. 物体A沿斜面向上运动的最大速度为![]()
【答案】BD
【解析】
开始时弹簧处于压缩状态,满足F弹1=mgsin300=kx1,即弹簧被压缩![]() ;则刚释放B的瞬时,系统的加速度满足:mg=2ma,即a=0.5g,方向沿斜面向上;由对称性可知,物体B运动到最低点时,A的加速度沿斜面向下,大小为0.5g,B的加速度向上,大小为0.5g,则对B分析可知,细绳上的拉力为T=mg+ma=1.5mg,选项A错误;弹簧恢复原长时,弹力为零,对AB的整体,由牛顿第二定律:mg-mgsin300=2ma2解得a2=0.25g,方向向下;对B:mg-T=ma2,解得细绳上的拉力为T=
;则刚释放B的瞬时,系统的加速度满足:mg=2ma,即a=0.5g,方向沿斜面向上;由对称性可知,物体B运动到最低点时,A的加速度沿斜面向下,大小为0.5g,B的加速度向上,大小为0.5g,则对B分析可知,细绳上的拉力为T=mg+ma=1.5mg,选项A错误;弹簧恢复原长时,弹力为零,对AB的整体,由牛顿第二定律:mg-mgsin300=2ma2解得a2=0.25g,方向向下;对B:mg-T=ma2,解得细绳上的拉力为T=![]() mg,选项B正确;系统在平衡位置时A的速度最大,在平衡位置时满足:mg= mgsin300+F弹2,解得F弹2=0.5mg;此时弹簧伸长
mg,选项B正确;系统在平衡位置时A的速度最大,在平衡位置时满足:mg= mgsin300+F弹2,解得F弹2=0.5mg;此时弹簧伸长![]() ,此位置弹簧的弹性势能与初始位置的弹性势能相同;由动能定理:
,此位置弹簧的弹性势能与初始位置的弹性势能相同;由动能定理:![]() ,解得
,解得 ![]() ,选项C错误,D正确;故选BD.
,选项C错误,D正确;故选BD.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目