题目内容
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为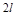
和
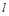，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示。开始时OA边处于水平位置，由静止释放，则
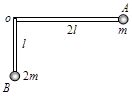
A.转动过程中A球的机械能守恒
B.转动过程中两球的机械能守恒
C.A球速度最大时，两小球的总重力势能最小
D.A、B两球的最大速度之比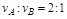
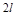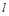和，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示。开始时OA边处于水平位置，由静止释放，则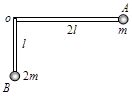 A.转动过程中A球的机械能守恒
B.转动过程中两球的机械能守恒
C.A球速度最大时，两小球的总重力势能最小
D.A、B两球的最大速度之比
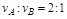
BCD
试题分析：在转动过程中支架可绕固定轴O在竖直平面内无摩擦转动，杆对系统做功为零，没有其他能量产生，所以系统机械能守恒，但对于A、B球来说由于有杆做功，所以两球各自的机械能都不守恒，B对；A错；当A球速度最大时B球速度也最大，但机械能不变，系统总重力势能最小，C对；两球围绕同一个转轴运动，所以角速度相同，由v=wr可知线速度之比等于半径之比，为2：1，D对；
点评：本题难度较小，明确机械能守恒的条件，了解机械能守恒的几种表达式，例如系统动能的增量的等于重力势能的减小量
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
平抛，小球碰到轨道后不反弹（沿轨道径向速度减为0），忽略一切阻力，求：
的固定光滑斜面上，而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑，M＝3m，开始时，将M抬高到A点，使细绳水平，此时OA段绳长为L＝4.0m，现M由静止开始下滑，求：当M下滑3.0m至B点时的速度为多大?（g取10m/s2）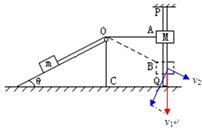
、
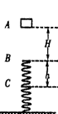
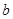两点分别是圆周的最高点和最低点，则下列说法中错误的是（ ）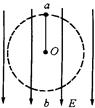
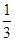g竖直下落到地面，在此过程中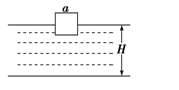
)
)
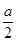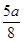