题目内容
【题目】如图所示,内壁光滑、截面积不相等的圆柱形气缸竖直放置,气缸上、下两部分的横截面积分别为2S和S.在气缸内有A、B两活塞封闭着一定质量的理想气体,两活塞用一根长为l的细轻杆连接,两活塞导热性能良好,并能在气缸内无摩擦地移动.已知活塞A的质量是2m,活塞B的质量是m.当外界大气压强为p0、温度为T0时,两活塞静止于如图所示位置.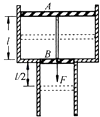
(1)求此时气缸内气体的压强.
(2)若用一竖直向下的拉力作用在B上,使A、B一起由图示位置开始缓慢向下移动 ![]() 的距离,又处于静止状态,求这时气缸内气体的压强及拉力F的大小.设整个过程中气体温度不变.
的距离,又处于静止状态,求这时气缸内气体的压强及拉力F的大小.设整个过程中气体温度不变.
【答案】
(1)解:以两活塞整体为研究对象,设此时气缸内气体压强为p1,根据平衡条件则有:
p0S+3mg=p1(2S﹣S)
解得:p1=p0+ ![]()
答:求此时气缸内气体的压强为p0+ ![]() .
.
(2)初态:p1=p0+ ![]() ,V1=2lS
,V1=2lS
末态:p2,V2= ![]() lS
lS
根据玻意耳定律有:(p0+ ![]() )2lS=p2(
)2lS=p2( ![]() lS)
lS)
解得:p2= ![]() (p0+
(p0+ ![]() )
)
以两活塞整体为研究对象,根据平衡条件有:p2S=F+p0S+3mg…②
解得F= ![]() +mg
+mg
答:这时气缸内气体的压强为 ![]() (p0+
(p0+ ![]() ),拉力F的大小为
),拉力F的大小为 ![]() +mg.
+mg.
【解析】(1)以两个活塞为研究对象,进行受力分析根据平衡条件列式求解。
(2)活塞开始缓慢向下移动的过程中,温度不变,属于等温变化。根据理想气体状态参量方程结合平衡条件列式子求解。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目