Question

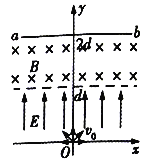
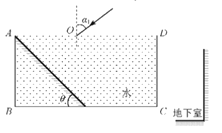
【题目】居家学习的某同学设计了一个把阳光导入地下室的简易装置。如图，ABCD为薄壁矩形透明槽装满水后的竖直截面，其中AB=d，AD=2d，平面镜一端靠在A处，与水平底面夹角θ=45°斜放入水槽。太阳光入射到AD面上，其中一细束光线以入射角53°射到水面上的O点，进入水中后，射到平面镜距A点为处。不考虑光的色散现象及水槽壁对光线传播的影响，取水对该束光的折射率，sin53°=，cos53°=。求该束光：

（i）射到平面镜时的入射角；

（ii）第次从水中射出的位置与D点的距离x。

Answer 1

【答案】（i）；（ii）

【解析】

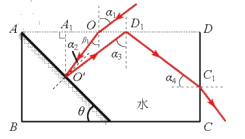
（i）光路图如图

设光线进入水面时的折射角为β1，由折射定律可得

①

②

由①②式及代入数据得

③

（ⅱ）设光射到平面镜的O′点，反射后射到水面的D1点，入射角为α3，由几何关系可得

α3=53°

AA1=O′A1

AD1=AA1+AD1=AO′cosθ+O′A1tanα3=④

DD1=AD-AD1=⑤

设光从水中射向空气的临界角为C，则

⑥

得

α3＞C⑦

光射到水面上D1点后将发生全反射，反射后到达CD面的C1点，此处入射角为α4

α4=90°-α3=37°⑧

由于α4＜C，光线从C1点射出水槽

⑨