题目内容
【题目】如图所示,足够大的空间区域内存在水平方向的匀强电场,场强大小为E。现将一带电的小球A用绝缘细线悬挂于O点,静止时小球位于P点,细线与竖直方向的夹角θ=30°。某时刻,将另一质量与A相同的不带电小球B,从与P等高的某点Q以初速度v0水平抛出,同时剪断细线,经过一段时间两球相遇。若相遇时两球速度方向相同,相遇后两球立即结合为一个小球。若在两球相遇的瞬间,将电场的方向反向,大小变为6E,再经相同时间,两小球的结合体运动到空间某点M(图中未画出)。已知重力加速度为g,求:
(1)小球A的比荷;
(2)Q 、P两点间的距离;
(3)P 、M两点间的距离。

【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)对带电小球A受力分析,如图所示:
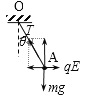
由平衡条件得: ![]() ,
, ![]()
解得: ![]()
(2) B球做平抛运动,相遇时两球速度方向相同得: ![]() ,
, ![]() ,
, ![]()
剪断后带电小球做初速度为零的匀加速直线运动,设在N点相遇,相遇时带电小球位移为![]() ,水平位移为
,水平位移为![]()
根据牛顿第二定律有: ![]()
相遇时带电小球的位移![]()
相遇时带电小球的水平位移![]()
设在PQ距离为![]() ,则有:
,则有: ![]()
(3)两球相遇时, ![]() ,
, ![]() ,
, ![]() ,两小球结合在一起时速度不变
,两小球结合在一起时速度不变
设两小球相遇后受力为大小为F,方向与竖直方向的夹角为![]() ,由力合成的平行四边形定则合力如图:
,由力合成的平行四边形定则合力如图:
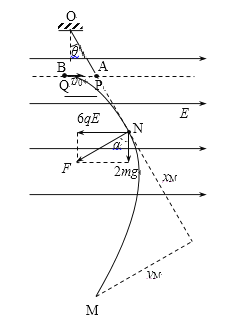
则有: ![]() ,解得:
,解得: ![]()
两小球结合体做初速度![]() 的类平抛运动,设加速度为
的类平抛运动,设加速度为![]() ,由牛顿第二定律得:
,由牛顿第二定律得: ![]()
设t时间内两小球结合体沿初速度方向发生的位移为![]() ,沿加速度方向发生的位移为
,沿加速度方向发生的位移为![]() ,由类平抛运动规律得:
,由类平抛运动规律得: ![]() ,
, ![]()
P、M间距为: ![]()
联立以上各式得: ![]()

练习册系列答案
相关题目