题目内容
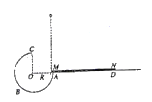
【题目】如图所示，一个四分之三圆弧形光滑圆轨道ABC放置在竖直平面内，轨道半径为R，在A点与水平桌面AD相接，桌面与圆心O等高。MN是放在水平桌面上长为3R、厚度不计的垫子，左端M正好位于A点。将一个质量为m、直径很小（可视为质点）的小球从A处正上方某点由静止释放，恰好可以沿A点切线方向进入圆轨道，不考虑空气阻力。欲使小球能通过C点落到垫子上，求小球离A点的高度的范围。
【答案】
【解析】
根据重力提供向心力求出小球经过C点的最小速度，然后根据平抛运动知识求出射程；在根据恰好射到N点得到经过C点的最大速度；最后根据机械能守恒定律求初位置高度。
小球能通过C点，在C点最小速度v满足：
解得：
小球离开C点做平抛运动，落到M点时间t为：
此时水平距离：
，小球能落在垫子上
小球在C点的最大速度为v′：
4R=v′t
解得：
设小球距离A点的高度为h，则小球运动到C点的过程中，有
由上可知，要使小球落在垫子上：
解得：
。
练习册系列答案
相关题目
