题目内容
一物体以一定的初速度,沿倾角可在0-90°之间任意调整的木板向上滑动,设它沿木板向上能达到的最大位移为x.若木板倾角不同时对应的最大位移x与木板倾角α的关系如图所示.g取10m/s2.求:
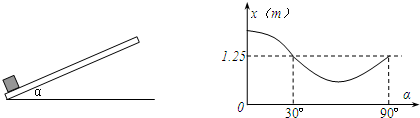
(1)物体初速度的大小v0.
(2)物体与木板间的动摩擦因数为μ.
(3)当α=60°时,它沿木板向上能达到的最大位移为x?
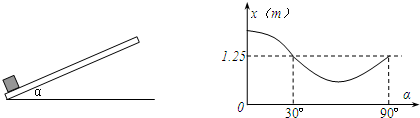
(1)物体初速度的大小v0.
(2)物体与木板间的动摩擦因数为μ.
(3)当α=60°时,它沿木板向上能达到的最大位移为x?
(1)当α=90°时,x=1.25m,物体做竖直上抛运动,根据动能定理,有:
mgx=
m
解得:v0=
=
=5m/s
(2)当α=30°时,x=1.25m
根据速度位移关系公式,有:
a=
=
m/s2=10m/s2
根据牛顿第二定律,有:
a=g(sin30°+μcos30°)
联立解得:μ=
;
(3)当α=60°时,根据牛顿第二定律,有:
a1=g(sin60°+μcos60°)=
m/s2
根据速度位移关系公式,有:
x=
=
=1.0825m
答:(1)物体初速度的大小为5m/s.
(2)物体与木板间的动摩擦因数为
.
(3)当α=60°时,它沿木板向上能达到的最大位移为x为1.0825m.
mgx=
| 1 |
| 2 |
| v | 20 |
解得:v0=
| 2gx |
| 2×10×1.25 |
(2)当α=30°时,x=1.25m
根据速度位移关系公式,有:
a=
| ||
| 2x |
| 52 |
| 2×1.25 |
根据牛顿第二定律,有:
a=g(sin30°+μcos30°)
联立解得:μ=
| ||
| 3 |
(3)当α=60°时,根据牛顿第二定律,有:
a1=g(sin60°+μcos60°)=
20
| ||
| 3 |
根据速度位移关系公式,有:
x=
| ||
| 2a1 |
5
| ||
| 8 |
答:(1)物体初速度的大小为5m/s.
(2)物体与木板间的动摩擦因数为
| ||
| 3 |
(3)当α=60°时,它沿木板向上能达到的最大位移为x为1.0825m.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?东城区三模)如图所示,一物体以一定的初速度沿水平地面从A点滑到B点,摩擦力做功为W1;若该物体从A′点沿两斜面滑到B′点(物体始终没有离开斜面),摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
(2010?东城区三模)如图所示,一物体以一定的初速度沿水平地面从A点滑到B点,摩擦力做功为W1;若该物体从A′点沿两斜面滑到B′点(物体始终没有离开斜面),摩擦力做的总功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
 如图,一物体以一定的初速度沿水平面由A点滑到B点,摩擦力做功为W1;若该物体从A′点沿斜面滑到B′点,摩擦力做功为W2,已知物体与各接触面的动摩擦因数均相同,则( )
如图,一物体以一定的初速度沿水平面由A点滑到B点,摩擦力做功为W1;若该物体从A′点沿斜面滑到B′点,摩擦力做功为W2,已知物体与各接触面的动摩擦因数均相同,则( )