题目内容
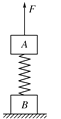
【题目】如图所示,质量M=4kg的小车长L=1.4m,静止在光滑水平面上,其上面右端静止一质量m=1kg的小滑块(可看作质点),小车与木板间的动摩擦因数μ=0.4,先用一水平恒力F向右拉小车。(g=10 m/s2.)
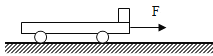
(1)若用一水平恒力F=10N,小滑块与小车间的摩擦力为多大?
(2)小滑块与小车间不发生相对滑动的水平恒力F大小要满足的条件?
(3)若用一水平恒力F=28N向右拉小车,要使滑块从小车上恰好滑下来,力F至少应作用多长时间
【答案】(1)2N;(2)20N;(3)1s
【解析】
试题分析:(1)当F=10N时,设两者间保持相对静止,
由整体法可得:F=(M+m)a1 得a1=2m/s2
隔离小滑块可得:f=ma1=2N
而两者间的最大静摩擦力为fmax=μmg=4N 所以小滑块与小车间的摩擦力为2N。
(2)当两者要发生相对滑动时,小滑块与小车间应达到最大的静摩擦力。此时小滑块的加速度可由fmax=μmg= m a2 得a2=4 m/s2
由整体法可得:F=(M+m)a2=20N
(3)当F=28N时,两者间相对滑动, 小滑块μmg= m a2 a2=4 m/s2
小车 F-μmg = Ma3 得: a3=6m/s2
设 F撤去前作用了时间t1,则两者获得的速度为![]() ,
,![]()
两者产生的位移为:![]()
F撤去后m仍以a2加速,M以a4减速,减速的加速度为![]()
设过时间t2两者等速![]() 代入得
代入得 ![]()
t2时间内位移 ![]()
![]() 得
得![]() 得t1=1s
得t1=1s
考点:牛顿第二定律、匀变速直线运动

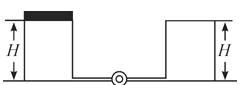
【题目】某同学验证动能定理的实验装置如图甲所示.水平桌面上固定一倾斜的气垫导轨;导轨上A点处有一带遮光片的长方形滑块,其总质量为M,实验步骤如下:
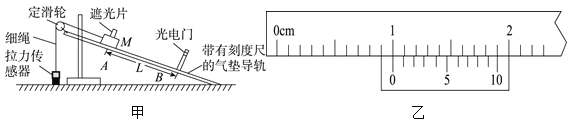
①用游标卡尺测出遮光片的宽度d;
②安装好实验器材,给气垫导轨接上气源,然后读出拉力传感器的示数,记为F,同时从气垫导轨刻度尺上读出滑块与光电门之间的距离L;
③剪断细绳,让滑块滑向光电门,并记录滑块通过光电门的时间t;
④多次改变滑块与光电门之间的距离,记录相应的L与t的值,结果如下表所示:
1 | 2 | 3 | 4 | 5 | |
L(m) | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
t(ms) | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
试分析下列问题:
(1)用游标卡尺测量遮光片宽度d的测量结果如图乙所示,则d=________cm.
(2)剪断细绳后,滑块开始加速下滑,则其受到的合外力为________.
(3)剪断细绳后,在滑块从A运动至B的过程中,合外力对滑块、遮光片组成的系统做的功可表示为W=_____,动能的增加量可表示为ΔEk=________;若动能定理成立,则在本实验中![]() 与L的关系式为
与L的关系式为![]() =________.
=________.