题目内容
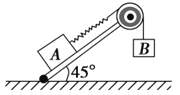
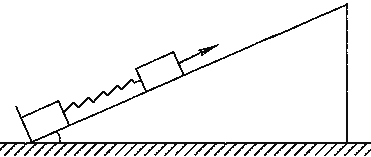
【题目】如图所示,质量![]() 、长L=6.0m的长板置于水平面上,质量
、长L=6.0m的长板置于水平面上,质量![]() 的小滑块置于长板A的左端,A与水平面的动摩擦因数
的小滑块置于长板A的左端,A与水平面的动摩擦因数![]() ,B与A间的动摩擦因数
,B与A间的动摩擦因数![]() ,对B施加一大小为
,对B施加一大小为![]() 、方向与水平面成37的恒力。最大静摩擦力等于滑动摩擦力,重力加速度
、方向与水平面成37的恒力。最大静摩擦力等于滑动摩擦力,重力加速度![]() ,sin37=0.6.cos37=0.8.
,sin37=0.6.cos37=0.8.

(1)求A、B的加速度大小;
(2)若力F作用一段时间后,撤去力F,B能从A的左端滑到右端,求力F作用的最短时间。
(3)力F的方向在什么范围内变化,可能使得:不论F多大,AB能保持相对静止且向右加速运动。(结果可用三角函数表示)
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)A 对B的最大静摩擦力fB=μ2(mBg-Fsin37°)=4N
地面对A的摩擦力为fA=μ1(mAg+mBg-Fsin37°)=5.4N
故A静止,aA=0
对B力分析,由牛顿第二定律可得有:Fcosθ-fAB=mBaB
Fsinθ+NAB=mBg
fAB=μNAB
解得aB=6m/s2
(2)撤去外力F时,B的速度为v0,此后B做匀减速运动用时t2,若B到达A的右端时恰好与A具有共同速度v,则力F的作用时间为t1最短
B做匀减速运动的加速度aB1=μ2g=5m/s2
A做加速运动的加速度为aA1=![]() =1m/s2
=1m/s2
v=v0-aB1t2
v=aA1t2
![]()
力F作用的最短时间t1=![]()
联立解得t1=1s
(3)设F斜向下,与水平方向夹角为![]() ,AB以相同的加速度a一起向右匀加速运动,AB之间的静摩擦力为f,则:
,AB以相同的加速度a一起向右匀加速运动,AB之间的静摩擦力为f,则:
![]()
![]()
解得:![]()
要求AB不发生相对滑动,需满足![]() 恒成立
恒成立
代入化简得:![]()
要求上式恒成立,需满足:![]()
要求AB一起向右匀加速,需要a>0
即:![]()
化简得:![]()
需满足: ![]()
代入数据得:![]()
综上,![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目