题目内容
17. 如图所示,一固定斜面的倾角为30°,C为斜面的最高点.轻弹簧一端固定在挡板A上,处于原长时另一端在B处,C、B两点间的高度差为h,质量为m的木箱(可看作质点)与斜面的动摩擦因数为$\frac{\sqrt{3}}{6}$,当地重力加速度为g.木箱从斜面顶端C无初速度下滑.下列选项正确的是( )
如图所示,一固定斜面的倾角为30°,C为斜面的最高点.轻弹簧一端固定在挡板A上,处于原长时另一端在B处,C、B两点间的高度差为h,质量为m的木箱(可看作质点)与斜面的动摩擦因数为$\frac{\sqrt{3}}{6}$,当地重力加速度为g.木箱从斜面顶端C无初速度下滑.下列选项正确的是( )| A. | 箱子最终将停在斜面上B点 | |
| B. | 箱子从C点运动到B点这一过程损失的机械能为$\frac{1}{2}$mgh | |
| C. | 箱子在斜面上运动的总路程等于4h | |
| D. | 箱子在整个运动过程中第一次通过B点时动能最大 |
分析 通过受力分析,可知得知箱子最后静止时,会受到弹簧的弹力作用,从而得知箱子的最终位置.箱子运动的过程中,损失的机械能即为摩擦力所做的功,通过功能关系可以得知从C到B的过程中,所损失的机械能.利用假设法,可知若最后停在B点,箱子通过的路程为4h,因箱子不会停在B点,从而判断路程会大于4h.
解答 解:A、木箱所受的摩擦力为:f=μmgcosθ=$\frac{\sqrt{3}}{6}$mgcos30°=$\frac{1}{4}$mg.因为mgsin30°>f,所以箱子与弹簧碰撞反弹上升至速度为零时会再次下滑,最后会在重力、支持力、弹簧的弹力和摩擦力的作用下处于静止状态,最终位置会低于B点,故A错误.
B、箱子从C点刚运动到B点的过程中,由能量的守恒可知损失的机械能为克服摩擦力所做的功,对箱子受力分析,受重力支持力和摩擦力,
沿斜面方向上的位移为:s=$\frac{h}{sin30°}$=2h,所以摩擦力所做的功为:Wf=fs=$\frac{1}{4}$mg×2h=$\frac{1}{2}$mgh,即损失的机械能为$\frac{1}{2}$mgh,故B正确.
C、假设箱子最终会停在B点,设此过程中箱子通过的路程为s,由能量守恒则有:mgh=μmgcosθ,代入数据得s=4h,对B的解答可知,箱子最终会停在B点一下,所以总路程会大于4h,故C错误.
D、箱子在整个运动过程中第一次通过B点时,由于mgsin30°>f,木箱仍向下加速运动,速度不是最大,故D错误.
故选:B.
点评 该题应用功能关系解答物理问题时,要注意对过程的分析,分析清楚在运动过程中有哪些力做功,以及这些力做功做功的特点,尤其是有摩擦力做功时,会有一定的机械能转化为内能,导致机械能不再守恒.这是在解题过程中应特别注意的一点.

 阅读快车系列答案
阅读快车系列答案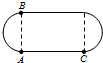 我国女运动员韦永丽在仁川亚运会赢得2金1银的好成绩.如图所示为田径运动场400m跑道示意图,可视为由两个半圆弧及两条长度均为100m的直线组成.在她参加的100m和200m的比赛中,100m比赛起点在A处,200m比赛起点在B处,终点均在C处,她的100m成绩为11.5s,200m成绩为23.3s,下列说法正确的是( )
我国女运动员韦永丽在仁川亚运会赢得2金1银的好成绩.如图所示为田径运动场400m跑道示意图,可视为由两个半圆弧及两条长度均为100m的直线组成.在她参加的100m和200m的比赛中,100m比赛起点在A处,200m比赛起点在B处,终点均在C处,她的100m成绩为11.5s,200m成绩为23.3s,下列说法正确的是( )| A. | 200m比赛的位移是100m比赛的两倍 | B. | 200m比赛的路程是100m比赛的两倍 | ||
| C. | 100m比赛冲刺时的速度为8.7m/s | D. | 200m比赛的平均速度为8.6m/s |
 半径R=1m的水平圆盘绕过圆心O的竖直轴匀速运动,A为圆盘边缘上一点.在O点的正上方将一个可视为质点的小球以初速度v0=2m/s水平抛出时,半径OA方向恰好与v0的方向相同,如图所示,若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度可能是( )
半径R=1m的水平圆盘绕过圆心O的竖直轴匀速运动,A为圆盘边缘上一点.在O点的正上方将一个可视为质点的小球以初速度v0=2m/s水平抛出时,半径OA方向恰好与v0的方向相同,如图所示,若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度可能是( )| A. | 2πrad/s | B. | 4πrad/s | C. | 6πrad/s | D. | 8πrad/s |
 将一质量为2.0kg的滑块置于一动摩擦因数μ=0.1的固定桌面上.将一水平拉力F作用在滑块上后,滑块由静止开始运动.如图是拉力F做的功与滑块运动位移之间的关系图.取g=10m/s2,则下列说法中正确的是( )
将一质量为2.0kg的滑块置于一动摩擦因数μ=0.1的固定桌面上.将一水平拉力F作用在滑块上后,滑块由静止开始运动.如图是拉力F做的功与滑块运动位移之间的关系图.取g=10m/s2,则下列说法中正确的是( )| A. | 滑块在0-3m的位移内受到的合外力为5N | |
| B. | 滑块在3-6m的位移内合外力做的功为12J | |
| C. | 图中AB段对应滑块做匀速直线运动 | |
| D. | 图中AB段对应滑块的动能在不断增加 |
 如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的物体沿斜面体的光滑斜面自由下滑时,斜面体仍静止不动.则斜面体( )
如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的物体沿斜面体的光滑斜面自由下滑时,斜面体仍静止不动.则斜面体( )| A. | 受地面的支持力为Mg | B. | 受地面的支持力为(m+M)g | ||
| C. | 受地面的摩擦力为mgcosθ | D. | 受地面的摩擦力为mgcosθsinθ |
| A. | 1:3 | B. | 1:12 | C. | 1:9 | D. | 1:6 |
 水平面上有两个质量相等的物体a和b,它们分别在水平推力F1和F2作用下开始运动,分别运动一段时间后撤去推力,两个物体都将运动一段时间后停下.物体的v-t图线如图所示,图中线段AB∥CD.则以下说法正确的是( )
水平面上有两个质量相等的物体a和b,它们分别在水平推力F1和F2作用下开始运动,分别运动一段时间后撤去推力,两个物体都将运动一段时间后停下.物体的v-t图线如图所示,图中线段AB∥CD.则以下说法正确的是( )