题目内容
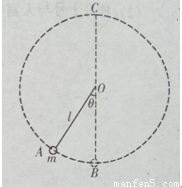
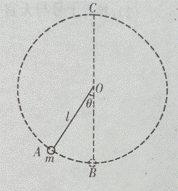
 不可伸长的轻绳长l=1.2m,一端固定在O点,另一端系一质量为m=2kg的小球.开始时,将小球拉至绳与竖直方向夹角θ=37°的A处,无初速释放,如图所示,取cos37°=0.8,g=10m/s2.
不可伸长的轻绳长l=1.2m,一端固定在O点,另一端系一质量为m=2kg的小球.开始时,将小球拉至绳与竖直方向夹角θ=37°的A处,无初速释放,如图所示,取cos37°=0.8,g=10m/s2.(1)求小球运动到最低点B时绳对球的拉力;
(2)若小球运动到B点时,对小球施加一沿速度方向的瞬时作用力F,让小球在竖直面内做完整的圆周运动,求F做功的最小值.
分析:(1)小球下摆过程中,机械能守恒,由机械能守恒定律可以求出到达B点的速度,由牛顿第二定律可以求出绳子的拉力;
(2)在C点由牛顿第二定律求出小球的速度,由动能定理求出力对小球做的功.
(2)在C点由牛顿第二定律求出小球的速度,由动能定理求出力对小球做的功.
解答:解:(1)小球从A到B过程中,由机械能守恒定律得:
mgl(1-cos37°)=
mv2,
在B点,由牛顿第二定律得:F-mg=m
,
解得:F=28N;
(2)小球通过最高点的速度为vc,
由牛顿第二定律:mg=m
从A到C的过程,由动能定理得:
W-mgl(1+cos37°)=
m
-0,
解得:W=55.2J;
答:(1)求小球运动到最低点B时绳对球的拉力为28N;(2)F做功的最小值为55.2J.
mgl(1-cos37°)=
| 1 |
| 2 |
在B点,由牛顿第二定律得:F-mg=m
| v2 |
| l |
解得:F=28N;
(2)小球通过最高点的速度为vc,
由牛顿第二定律:mg=m
| ||
| l |
从A到C的过程,由动能定理得:
W-mgl(1+cos37°)=
| 1 |
| 2 |
| v | 2 c |
解得:W=55.2J;
答:(1)求小球运动到最低点B时绳对球的拉力为28N;(2)F做功的最小值为55.2J.
点评:分析小球的运动过程,应用机械能守恒定律、牛顿第二定律、动能定理即可正确解题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
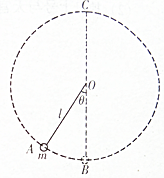
 如图所示,一不可伸长的轻绳长为L,一端固定在O点,另一端系着一个质量为m 的小球.开始小球处于A点细绳恰好拉直(绳中无拉力),现让小球由静止自由释放,则小球运动到O正下方的C点时绳子的拉力大小为( )
如图所示,一不可伸长的轻绳长为L,一端固定在O点,另一端系着一个质量为m 的小球.开始小球处于A点细绳恰好拉直(绳中无拉力),现让小球由静止自由释放,则小球运动到O正下方的C点时绳子的拉力大小为( )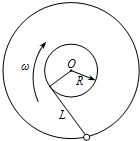 (2005?淮安模拟)如图所示,一条不可伸长的轻绳长为L,一端用手握住,另一端系一质量为m的小球.今使手握的一端在水平桌面上做半径为R,角速度为ω的匀速圆周运动,且使绳始终与半径为R的圆相切,小球也将在同一水平面内做匀速圆周运动,若人手做功的功率为P,求:
(2005?淮安模拟)如图所示,一条不可伸长的轻绳长为L,一端用手握住,另一端系一质量为m的小球.今使手握的一端在水平桌面上做半径为R,角速度为ω的匀速圆周运动,且使绳始终与半径为R的圆相切,小球也将在同一水平面内做匀速圆周运动,若人手做功的功率为P,求: