Question

【题目】如图，在金属导轨MNC和PQD中，MN与PQ平行且间距为L＝1 m，MNQP所在平面与水平面夹角α＝37°．N、Q连线与MN垂直，M、P间接有阻值R＝10 Ω的电阻．光滑直导轨NC和QD在同一水平面内，与NQ的夹角均为θ＝53°．ab棒的初始位置在水平导轨上与NQ重合．ef棒垂直放在倾斜导轨上，与导轨间的动摩擦因数为μ＝0．1，由导轨上的小立柱1和2阻挡而静止．金属棒ab和ef质量均为m＝0．5 kg，长均为L＝1 m．空间有竖直方向、磁感应强度B＝2 T的匀强磁场（图中未画出）．两金属棒与导轨保持良好接触，ef棒的阻值R＝10 Ω，不计所有导轨和ab棒的电阻．假设最大静摩擦力与滑动摩擦力大小相等．忽略感应电流产生的磁场．若ab棒在拉力F的作用下，以垂直于NQ的速度v1＝1 m/s在水平导轨上向右匀速运动，且运动过程中ef棒始终静止（g取10 m/s2，sin 37°＝0．6，cos 37°＝0．8）．

（1）求金属棒ab运动到x＝0．3 m处时，经过ab棒的电流大小；

（2）推导金属棒ab从NQ处运动一段距离x过程中拉力F与x的关系式；

（3）若ab棒以垂直于NQ的速度v2＝2 m/s在水平导轨上向右匀速运动，在NQ位置时取走小立柱1和2，且运动过程中ef棒始终静止．求此状态下磁感应强度B的最大值（此问结果可只保留一位有效数字）．

Answer 1

【答案】（1）0.22A

（2）

（3）4.79T；磁场方向可竖直向上，也可竖直向下。

【解析】

试题（1）ab棒滑行距离为x时，ab棒在导轨间的棒长

此时，ab棒产生的电动势

流过ab棒的电流

（2）拉力F与x的关系式，代入数据得

（3）流过ef棒的电流①

ef棒所受安培力②

联立①②，解得，③

由③式可得，在x＝0和B为最大值时有最大值

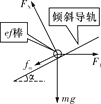
由题意知，ab棒所受安培力方向必水平向左，ef棒所受安培力方向必水平向右，使为最大值的受力分析如图所示，图中为最大静摩擦力，

则有：④

联立③④，代入数据得，