��Ŀ����
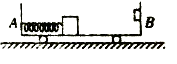
����Ŀ����ͼ��С��A���ڹ̶���ˮƽ���ϵĹ⻬��Բ�����ϣ�С��B��ˮƽ�ᵯ�����ţ����ɹ̶�����ֱ���ϣ���С��A��Bͨ���⻬����O������ϸ����������������ھ�ֹ״̬����֪��B����Ϊm��O���ڰ�Բ����Բ��O1�����Ϸ���OA����ֱ�����30��ǣ�OA�������Բ����뾶��ȣ�OB����ֱ�����45��ǣ��ֽ�����ϸ���ϵ�˲�䣨�������ٶ�Ϊg����������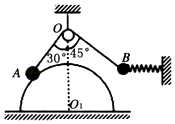
A.���ɵ�����С ![]() mg
mg
B.��B�ļ��ٶ�Ϊg
C.��A�ܵ���֧����Ϊ ![]() mg
mg
D.��A�ļ��ٶ�Ϊ ![]() g
g
���𰸡�D
���������⣺A�������B���������ݹ�����ƽ��ã�
ˮƽ�����У�TOBsin45��=F
��ֱ�����У�TOBcos45��=mg��
����TOB= ![]() mg
mg
���ɵ�Ϊ��F=mg��A���������⣮
B����B������������֪���ڼ���˲��B�ܵ��ĺ��� ![]() ������ţ�ٵڶ����ɿ�֪
������ţ�ٵڶ����ɿ�֪ ![]() ��B���������⣻
��B���������⣻
C����ͼ��ʾ���ɼ��ι�ϵ��֪����TOA��֧����N��ˮƽ����ļн���ȣ��н�Ϊ60�㣬
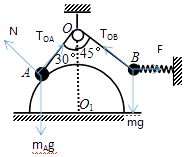
��N��TOA��ȣ��У�2TOAsin60��=mAg����� mA= ![]() m������������TOA=0����Բ�����߷�����ذ뾶����������˲���ٶ�Ϊ�㣬�ذ뾶�������Ϊ�㣬�У�
m������������TOA=0����Բ�����߷�����ذ뾶����������˲���ٶ�Ϊ�㣬�ذ뾶�������Ϊ�㣬�У�
N=mAgsin60��= ![]() mAg=
mAg= ![]() mg��C����������
mg��C����������
D������A�������߷������ţ�ٵڶ������У�a= ![]() =
= ![]() g��D���������⣮
g��D���������⣮
��ѡ��D
�ֱ��AB���������������������A���崦��ƽ��״̬��B���崦�ڷ�ƽ��״̬������ƽ��������ţ�ٵڶ��˶����ɣ���ʽ��⡣