题目内容
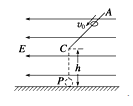
【题目】如图所示,水平放置的两个平行金属板,上板带负电,下板带等量的正电,三个质量相等,分别带正电.负电和不带电的质点从极板的左侧P点以相同的水平初速度进入电场中分别落在正极板的![]() 三处,由此可知( )
三处,由此可知( )

A.粒子a带正电,b不带电,c带负电
B.三个粒子在电场中运动的时间相等
C.三个粒子在电场中的加速度![]()
D.三个粒子到达正极板的动能![]()
【答案】D
【解析】
试题分析:根据题意,三小球在水平方向做匀速直线运动,则有![]() ,
,![]() 相同,则水平位移
相同,则水平位移![]() 与运动时间
与运动时间![]() 成正比,由图看出,水平位移的关系为
成正比,由图看出,水平位移的关系为![]() ,则运动时间关系为
,则运动时间关系为![]() ,竖直方向上三个粒子都做初速度为0的匀加速直线运动,到达下极板时,在竖直方向产生的位移y相等:
,竖直方向上三个粒子都做初速度为0的匀加速直线运动,到达下极板时,在竖直方向产生的位移y相等:![]() ,则知加速度关系为
,则知加速度关系为![]() ,由牛顿第二定律得知三个小球的合力关系为
,由牛顿第二定律得知三个小球的合力关系为![]() ,由于平行板间有竖直向上的电场,正电荷在电场中受到向上的电场力,向下的合力最小,向下的加速度最小,负电荷受到向下的电场力,向下的合力最大,向下的加速度最大,不带电的小球做平抛运动,加速度为重力加速度g,可知,落在a点的颗粒带负电,c点的带正电,b点的不带电,故ABC错误;由以上分析可知,
,由于平行板间有竖直向上的电场,正电荷在电场中受到向上的电场力,向下的合力最小,向下的加速度最小,负电荷受到向下的电场力,向下的合力最大,向下的加速度最大,不带电的小球做平抛运动,加速度为重力加速度g,可知,落在a点的颗粒带负电,c点的带正电,b点的不带电,故ABC错误;由以上分析可知,![]() ,则竖直位移相同,则可知外力做功a最大,c最小;则由动能定理可知三个粒子到达正极板的动能
,则竖直位移相同,则可知外力做功a最大,c最小;则由动能定理可知三个粒子到达正极板的动能![]() ,故D正确。
,故D正确。

【题目】因测试需要,一辆汽车在某雷达测速区,沿平直路面从静止开始匀加速直线运动一段时间后,即刻做匀减速直线运动直到最后停止。下表中给出了雷达测出的各个时刻对应的汽车速度数值。
时刻t/s | 0 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 | 16.0 | 18.0 |
速度υ/(m·s-1) | 0 | 4.8 | 9.6 | 14.4 | 17.0 | 13.0 | 9.0 | 5.0 | 1.0 | 0 |
(1)汽车做匀加速运动和匀减速运动的加速度a1、a2的大小分别是多少?
(2)汽车在该区域行驶过程中何时速度达到最大?最大速度υm是多少?
(3)汽车在该区域行驶过程中的总位移x是多少?