题目内容
11. 如图所示,竖直固定的管道内有一个小球,球的直径比管的内径稍小,管内内壁是粗糙的,管内外壁是光滑的,管道的半径为R,R远大于管的内径,小球在管的最低点,现给小球一个向右的初速度,使小球在管道里运动,为了使小球能在管道里越过最高点一直运动下去,小球在最低的初速度至少为(重力加速度为g)( )
如图所示,竖直固定的管道内有一个小球,球的直径比管的内径稍小,管内内壁是粗糙的,管内外壁是光滑的,管道的半径为R,R远大于管的内径,小球在管的最低点,现给小球一个向右的初速度,使小球在管道里运动,为了使小球能在管道里越过最高点一直运动下去,小球在最低的初速度至少为(重力加速度为g)( )| A. | $\sqrt{2gR}$ | B. | $\sqrt{3gR}$ | C. | $\sqrt{4gR}$ | D. | $\sqrt{5gR}$ |
分析 小球在最高点,靠重力和管道的弹力提供向心力,若使小球能在管道里越过最高点一直运动下去,则小球不能受到摩擦力的作用,所以管的外侧与小球之间有相互作用,而管的内侧始终与小球没有作用力,根据牛顿第二定律小球弹力和速度的关系.
解答 解:根据题意可知,小球与管的内壁之间始终不能有作用力,所以小球在最高点时,恰好又重力提供向心力时,对应的速度最小,此时:
$mg=\frac{m{v}_{min}^{2}}{\\;R}$
从最高点到最低点的过程中,重力做功,机械能守恒,得:
$mg•2R+\frac{1}{2}m{v}_{min}^{2}=\frac{1}{2}m{v}^{2}$
联立得:
v=$\sqrt{5gR}$
故选:D
点评 解决本题的关键知道小球做圆周运动向心力的来源,运用牛顿第二定律进行求解,该模型与杆模型类似,与绳模型不同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.许多科学家在物理发展过程中做出了重要贡献,下列表述正确的是( )
| A. | 亚里士多德认为力是维持物体运动状态的原因 | |
| B. | 开普勒通过万有引力定律推导出了开普勒三定律 | |
| C. | 牛顿站在巨人的肩上,发现了万有引力定律,并且利用万有引力定律首次计算出了地球的质量 | |
| D. | 胡克认为只有在一定的条件下,弹簧的弹力与弹簧的形变量成正比 |
16.下列说法中不正确的是( )
| A. | 第一宇宙速度是人造地球卫星运行最大环绕速度,也是发射卫星所需最小发射速度 | |
| B. | 当卫星速度达到11.2 km/s,卫星就能脱离地球的束缚 | |
| C. | 第一宇宙速度等于7.9km/s,它是卫星在地球表面附近绕地球做匀速圆周运动的线速度的大小 | |
| D. | 地球同步卫星的运行速度大于第一宇宙速度 |
3.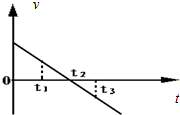 如图所示,作直线运动的物体在t1、t3两时刻对应的纵坐标绝对值相同,下列说法不正确的是( )
如图所示,作直线运动的物体在t1、t3两时刻对应的纵坐标绝对值相同,下列说法不正确的是( )
 如图所示,作直线运动的物体在t1、t3两时刻对应的纵坐标绝对值相同,下列说法不正确的是( )
如图所示,作直线运动的物体在t1、t3两时刻对应的纵坐标绝对值相同,下列说法不正确的是( )| A. | t1、t3两时刻速度相同 | B. | t2时刻速度和加速度均为零 | ||
| C. | t1、t3两时刻加速度等值反向 | D. | 图象中各时刻加速度均相同 |
20.一列简谐横波在某一时刻的波形图如图甲所示,图乙是横坐标为x=1.5m的P质点的振动图象.则( )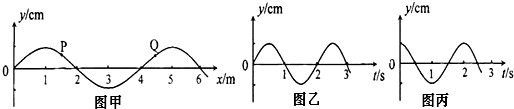

| A. | 这列简谐波的波速一定是2m/s | |
| B. | 若图甲为开始计时后0.25s的波形图,则波向x轴负方向传播 | |
| C. | 若波沿x轴正方向传播,同时一个观察者从6m处沿x轴负方向运动,他接收到波的频率小于0.5Hz | |
| D. | Q点是x=4.5m的质点,其的振动图象一定是图丙 |
1.如图所示,把光滑斜面上物体的重力mg分解为F1、F2两个力,下列说法正确的是( )


| A. | F1是斜面作用在物体上使物体下滑的力,F2是物体对斜面的压力 | |
| B. | 物体受到mg、FN、F1、F2共4个力作用 | |
| C. | 物体受到的合力为mgsinθ,方向沿斜面向上 | |
| D. | 力FN、F1、F2这3个力的作用效果和mg与FN两个力的作用效果相同 |
 做“探究求合力的方法”实验.如图所示,用A、B两弹簧秤拉橡皮条,使其伸长到O点.现保持夹角α不变,夹角β减小(α、β均为锐角且α+β>90°),同时适当调整弹簧秤A、B的拉力大小,可使O点保持不变,这时:
做“探究求合力的方法”实验.如图所示,用A、B两弹簧秤拉橡皮条,使其伸长到O点.现保持夹角α不变,夹角β减小(α、β均为锐角且α+β>90°),同时适当调整弹簧秤A、B的拉力大小,可使O点保持不变,这时: