��Ŀ����
1��һλͬѧ�����߲���ݣ������ȴӾ�ֹ��ʼ���ȼ��١��ȼ����˶��ɵײ����������㣬���ﶥ��ʱ�ٶ�ǡ��Ϊ�㣬������ʱ��ΪT1���˶������е�����ٶ�ΪV0�������ٴӾ�ֹ��ʼ���ȼ��٣����٣��ȼ����˶��ɶ����½����ײ㣬����ײ�ʱ�ٶ�ǡ��ҲΪ�㣬�½���ʱ��ΪT2���˶�����������ٶ�Ϊ$\frac{{V}_{0}}{2}$���������������˶��ͼ����˶��ļ��ٶȴ�С��ȣ����½�ʱ�ļ��ٶȵĴ�С������ʱ�ļ��ٶȴ�С��һ�룬���ֵT1��T2������ ������ʱ�ļ��ٶ�Ϊa�����½�ʱ�ļ��ٶ�Ϊ$\frac{a}{2}$�������ٶ�ʱ���ϵ��λ��ʱ���ϵ������⼴�ɣ�
��� �⣺������ʱ�ļ��ٶ�Ϊa�����½�ʱ�ļ��ٶ�Ϊ$\frac{a}{2}$��
������ʱ��ʱ��${T}_{1}=\frac{{v}_{0}}{a}+\frac{{v}_{0}}{a}=\frac{2{v}_{0}}{a}$�������ľ���$h=\frac{{v}_{0}^{2}}{2a}+\frac{{v}_{0}^{2}}{2a}=\frac{{v}_{0}^{2}}{a}$
�½�ʱ�ļ���ʱ��${t}_{2}=\frac{\frac{{v}_{0}}{2}}{\frac{a}{2}}=\frac{{v}_{0}}{a}$�������½���λ��${h}_{2}=\frac{��\frac{{v}_{0}^{\;}}{2}��^{2}}{2��\frac{a}{2}}=\frac{{v}_{0}^{2}}{4a}$
�½�ʱ�ļ����˶�ʱ��${t}_{2}��=\frac{\frac{{v}_{0}}{2}}{\frac{a}{2}}=\frac{{v}_{0}}{a}$�������½���λ��${h}_{2}��=\frac{��\frac{{v}_{0}}{2}��^{2}}{2��\frac{a}{2}}=\frac{{v}_{0}^{2}}{4a}$
���������½���λ��${h}_{2}��=h-{h}_{2}-{h}_{2}��=\frac{{v}_{0}^{2}}{2a}$�������½���ʱ��${t}_{2}��=\frac{{h}_{2}��}{\frac{{v}_{0}}{2}}=\frac{{v}_{0}}{a}$
�����½�����ʱ��${T}_{2}={t}_{2}+{t}_{2}��+{t}_{2}��=\frac{3{v}_{0}}{a}$
���Կɵã�$\frac{{T}_{1}}{{T}_{2}}=\frac{2}{3}$
�𣺱�ֵT1��T2=2��3��
���� ���ն����ֱ���˶����ٶ�ʱ���ϵ��λ��ʱ���ϵ����ȷ����Ĺؼ����������ڻ����⣮

 �϶����������2011��6��9��16ʱ50��05����̽���������������������������2�������յ�������̽�⣮8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150����Զ����������L2�㣮��ͼ��ʾ�����϶�������ǡ�����̫��ʼ����һ��ֱ���ϣ��͵���һͬ��̫����ת������������ȷ���ǣ�������
�϶����������2011��6��9��16ʱ50��05����̽���������������������������2�������յ�������̽�⣮8��25��23ʱ27�֣�����77��ķ��У����϶���š����������״�ʵ�ִ��������������ܿ�ȷ����������Լ150����Զ����������L2�㣮��ͼ��ʾ�����϶�������ǡ�����̫��ʼ����һ��ֱ���ϣ��͵���һͬ��̫����ת������������ȷ���ǣ�������| A�� | �϶���ŵļ��ٶȴ��ڵ���ļ��ٶ� | |
| B�� | �϶���ŵ����ٶ�С�ڵ�������ٶ� | |
| C�� | �϶������̫����ת�����ڴ���һ�� | |
| D�� | �϶�������������������̫���ṩ |
 ��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P������ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������
��ͼ��ʾ��������������ȣ��ֱ�����硢����Ͳ������С��ƽ�а�糡��˵��е�P������ͬ�ij��ٶ���ˮƽ����ֱ�ڵ糡�������糡�����Ƿֱ�����A��B��C���㣬�����жϣ�������| A�� | С��A�����磬B�����磬C������ | |
| B�� | С��A�����磬B�����磬C������ | |
| C�� | ����С���ڵ糡���˶��ļ��ٶ���ͬ | |
| D�� | ����С���ڵ糡���˶�ʱ����ȣ���ΪС�����ֱλ����ͬ |

| A�� | v=��4+2t��m/s | B�� | v=��-4+2t��m/s | C�� | x=��-4t+t2��m | D�� | x=��-4t-t2��m/s |
| A�� | �����ڲ��糡ǿ��һ��Ϊ0 | |
| B�� | ����ĵ���һ��Ϊ0 | |
| C�� | ���������ڲ��ĵ������ | |
| D�� | �������ĵ��ƿ��ܴ����ڲ��ĵ��� |
 ��ͼ��ʾ����ֱ�̶��Ĺܵ�����һ��С�����ֱ���ȹܵ��ھ���С�������ڱ��Ǵֲڵģ���������ǹ⻬�ģ��ܵ��İ뾶ΪR��RԶ���ڹܵ��ھ���С���ڹܵ���͵㣬�ָ�С��һ�����ҵij��ٶȣ�ʹС���ڹܵ����˶���Ϊ��ʹС�����ڹܵ���Խ����ߵ�һֱ�˶���ȥ��С������͵ij��ٶ�����Ϊ���������ٶ�Ϊg����������
��ͼ��ʾ����ֱ�̶��Ĺܵ�����һ��С�����ֱ���ȹܵ��ھ���С�������ڱ��Ǵֲڵģ���������ǹ⻬�ģ��ܵ��İ뾶ΪR��RԶ���ڹܵ��ھ���С���ڹܵ���͵㣬�ָ�С��һ�����ҵij��ٶȣ�ʹС���ڹܵ����˶���Ϊ��ʹС�����ڹܵ���Խ����ߵ�һֱ�˶���ȥ��С������͵ij��ٶ�����Ϊ���������ٶ�Ϊg����������| A�� | $\sqrt{2gR}$ | B�� | $\sqrt{3gR}$ | C�� | $\sqrt{4gR}$ | D�� | $\sqrt{5gR}$ |
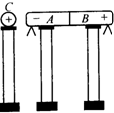 ��ͼ��ʾ�����о���Ӧ����ʵ���У�A��BΪ��Ӵ����þ�Ե֧��֧�ֵĽ������壬������Dz����磬�����ǵ��²����н�����Ƭ��C�Ǵ������С���������в���ʱ�ῴ��������������ſ����պϡ���
��ͼ��ʾ�����о���Ӧ����ʵ���У�A��BΪ��Ӵ����þ�Ե֧��֧�ֵĽ������壬������Dz����磬�����ǵ��²����н�����Ƭ��C�Ǵ������С���������в���ʱ�ῴ��������������ſ����պϡ��� ����ͼ��ʾ��·�У���Դ�綯��E=15V������r=1.0������ֵ����R1=29����R2=30����R3=60���������رպϺ���R3�����ĵĵ繦���Ƕ��
����ͼ��ʾ��·�У���Դ�綯��E=15V������r=1.0������ֵ����R1=29����R2=30����R3=60���������رպϺ���R3�����ĵĵ繦���Ƕ��