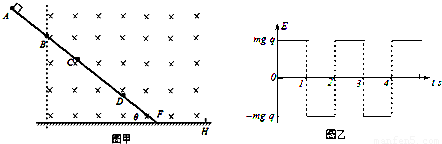题目内容
如图1所示,一个三角形物块固定在水平桌面上,其光滑斜面的倾角为θ=30°.物体A的质量为mA=0.5㎏,物体B的质量为mB=1.0㎏(A、B均可视为质点),物体A、B并列在斜面上且压着一劲度系数为k=125N/m的轻弹簧,弹簧的下端固定,上端拴在A物体上,物体A、B处于静止状态.(g取10m/s2)
(1)求此时弹簧的压缩量是多大?
(2)将物体B迅速移开,A运动到平衡位置时弹簧的压缩量是多大?
(3)将物体B迅速移开,物体A将作周期为0.4s的简谐振动,若以沿斜面向上的方向为正方向,请你在所给的坐标系(图2)中作出物体A相对平衡位置的位移随时间的变化曲线图,并在图中标明振幅的大小(至少画一个周期).

(1)求此时弹簧的压缩量是多大?
(2)将物体B迅速移开,A运动到平衡位置时弹簧的压缩量是多大?
(3)将物体B迅速移开,物体A将作周期为0.4s的简谐振动,若以沿斜面向上的方向为正方向,请你在所给的坐标系(图2)中作出物体A相对平衡位置的位移随时间的变化曲线图,并在图中标明振幅的大小(至少画一个周期).

分析:(1)对AB整体受力分析,受重力、支持力和弹簧的弹力,根据平衡条件列式求解;
(2)找出新的平衡位置后得到振幅,然后作图;
(3)简谐运动回复力与位移满足F=-kx关系.
(2)找出新的平衡位置后得到振幅,然后作图;
(3)简谐运动回复力与位移满足F=-kx关系.
解答:解:(1)物体A、B在斜面上处于平衡状态,所受外力平衡,设压缩量为x,则有:
(mA+mB)gsin30°=kx
解得:x=
=0.06m
(2)将物体B移开后,物体A作简谐运动的振幅为:A=
=0.04m
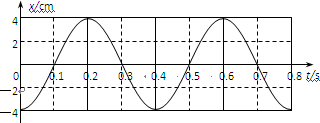
已知系统的振动周期为T=0.4s,振动的位移随时间的变化关系曲线如下图:
(3)设物体A在平衡位置时弹簧的压缩量为x0,则有mAgsinθ=kx0,当物体A经过平衡位置下方的某一位置时,
对平衡位置的位移的大小为x,则:F=k(x0-x)-mAgsinθ
由以上两式得:F=-kx且位移的方向与F的方向相反.即物体A作简谐运动.
答:(1)此时弹簧的压缩量是0.06m;
(2)如图所示;
(3)证明如上.
(mA+mB)gsin30°=kx
解得:x=
| (mA+mB)gsin30° |
| k |
(2)将物体B移开后,物体A作简谐运动的振幅为:A=
| mBgsin30° |
| k |
已知系统的振动周期为T=0.4s,振动的位移随时间的变化关系曲线如下图:

(3)设物体A在平衡位置时弹簧的压缩量为x0,则有mAgsinθ=kx0,当物体A经过平衡位置下方的某一位置时,
对平衡位置的位移的大小为x,则:F=k(x0-x)-mAgsinθ
由以上两式得:F=-kx且位移的方向与F的方向相反.即物体A作简谐运动.
答:(1)此时弹簧的压缩量是0.06m;
(2)如图所示;
(3)证明如上.
点评:本题关键明确物体做简谐运动的动力学条件是回复力与位移满足F=-kx关系,同时结合共点力平衡条件列式求解.

练习册系列答案
相关题目

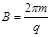 。现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为
。现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为 ,t=2s时刻,物体滑动到B点。在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s。(物体所受到的洛伦兹力小于2mgcosθ)
,t=2s时刻,物体滑动到B点。在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s。(物体所受到的洛伦兹力小于2mgcosθ) ,求物块滑动到B的速度大小。
,求物块滑动到B的速度大小。

 。现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为
。现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为 ,t=2s时刻,物体滑动到B点。在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s。(物体所受到的洛伦兹力小于2mgcosθ)
,t=2s时刻,物体滑动到B点。在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s。(物体所受到的洛伦兹力小于2mgcosθ) ,求物块滑动到B的速度大小。
,求物块滑动到B的速度大小。

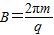 .现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为μ,t=2s时刻,物体滑动到B点.在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s.(物体所受到的洛伦兹力小于2mgcosθ)
.现有一个质量为m,电量为q的带正电的物体(可以视为质点),在t=0时从A点静止释放,物体与轨道间的动摩擦因数为μ,t=2s时刻,物体滑动到B点.在B点以后的运动过程中,物体没有离开磁场区域,物体在轨道上BC段的运动时间为1s,在轨道上CD段的运动时间也为1s.(物体所受到的洛伦兹力小于2mgcosθ)